Hostname: page-component-66644f4456-q629f Total loading time: 0 Render date: 2025-02-12T21:31:48.791Z Has data issue: true hasContentIssue false
  • English
  • Franรงais

On Locating Isometric ๐“(n)1

Published online by Cambridge University Press:ย  20 November 2018

Anthony Weston
Anthony Weston*
Affiliation:
Department of Mathematics and Statistics Canisius College, Buffalo, New York 14208 USA, e-mail: weston@canisius.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the โ€˜Save PDFโ€™ action button.

Motivated by a question of Per Enflo, we develop a hypercube criterion for locating linear isometric copies of 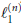$\ell _{1}^{\left( n \right)}$ in an arbitrary real normed space 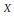$X$.

The said criterion involves finding 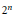${{2}^{n}}$ points in 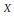$X$ that satisfy one metric equality. This contrasts nicely to the standard classical criterion wherein one seeks $n$ points that satisfy 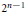${{2}^{n-1}}$ metric equalities.

Keywords

46B0405C1005B99Normed spaceshypercubes
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 3 , 01 September 2001 , pp. 370 - 375
Copyright
Copyright ยฉ Canadian Mathematical Society 2001

References

[BMW] Bourgain, J., Milman, V. and Wolfson, H., On type of metric spaces. Trans. Amer.Math. Soc. 294 (1986), 295โ€“317.Google Scholar
[DL] Deza, M. M. and Laurent, M., Geometry of Cuts and Metrics. Algorithms and Combinatorics 15(1997), Springer Verlag, 1โ€“600.Google Scholar
[E] Enflo, P., On the non-existence of uniform homeomorphisms between Lp-spaces. Ark.Mat. 8 (1969), 103โ€“105.Google Scholar
[LTW1] Lennard, C., Tonge, A. and Weston, A., Generalized roundness and negative type. Michigan J. Math. 44 (1997), 37โ€“45.Google Scholar
[LTW2] Lennard, C., Tonge, A. and Weston, A., Roundness and metric type. J. Math. Anal. Appl. (to appear in 2000), 1โ€“10.Google Scholar
[L] Lรถvblom, G.-M., Uniform homeomorphisms between unit balls in Lp-spaces, Math. Scand. 62 (1988), 294โ€“302.Google Scholar
[P] Pisier, G., Probabilistic Methods in the Geometry of Banach Spaces. Springer LectureNotes in Math. 1206 (1985), 1โ€“75.Google Scholar
[W] Weston, A., A non-linear l1 problem. Quaestiones Math. 20 (1997), 605โ€“610.Google Scholar