Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-24T23:01:00.987Z Has data issue: false hasContentIssue false
  • English
  • Français

On Minimally Thin Sets in a Stolz Domain

Published online by Cambridge University Press:  20 November 2018

H. L. Jackson
H. L. Jackson*
Affiliation:
McMaster University, Hamilton, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let D denote the open right half plane and

a Stolz domain in D with vertex at the origin. If h is a minimal harmonic function on D with pole at the origin then E⊂D is minimally thin at the origin iff where 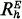is the reduced function of h on E in the sense of Brelot. We now define

where s shall be fixed to be 1/e. For the set E∩In we shall let cn denote the outer ordinary capacity (see [1, pp. 320-321]), An the outer logarithmic capacity, and on the outer Green capacity with respect to D. If E⊂K, Mme. Lelong [3, p. 131] was able to prove that E is minimally thin at the origin Since one cannot easily relate the classical measure theoretic properties of a plane set with its Green capacity, it would appear desirable to find some other criteria for minimal thinness.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 15 , Issue 2 , June 1972 , pp. 219 - 223
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Brelot, M., Points irréguliers et transformations continues en théorie du potentiel, J. Math. Pure. App. 19 (1940), 319-337.Google Scholar
2. Jackson, H. L., Some results on thin sets in a half-plane, Ann. Inst. Fourier (Grenoble) (2) 20 (1970), 201-218.Google Scholar
3. Lelong, J., étude au voisinage de la frontière des fonctions surharmoniques positives dans un demi-espace, Ann. de L'école Normale Sup. 66 (1949), 125-159.Google Scholar
4. Tsuji, M., Potential theory in modem function theory, Maruzen, Tokyo, 1959.Google Scholar