Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T04:51:10.548Z Has data issue: false hasContentIssue false
  • English
  • Français

On Modules Whose Proper Homomorphic Images Are of Smaller Cardinality

Published online by Cambridge University Press:  20 November 2018

Greg Oman  and
Adam Salminen
Greg Oman
Affiliation:
Department of Mathematics, The University of Colorado at Colorado Springs, Colorado Springs, CO 80918, USAe-mail: goman@uccs.edu
Adam Salminen
Affiliation:
Department of Mathematics, University of Evansville, Evansville, IN 47722, USAe-mail: as341@evansville.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $R$ be a commutative ring with identity, and let 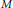$M$ be a unitary module over $R$. We call 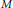$M$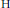$\text{H}$-smaller (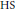$\text{HS}$ for short) if and only if 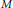$M$ is infinite and 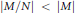$\left| M/N \right|\,<\,\,\left| M \right|$ for every nonzero submodule 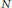$N$ of 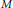$M$. After a brief introduction, we show that there exist nontrivial examples of HS modules of arbitrarily large cardinality over Noetherian and non-Noetherian domains. We then prove the following result: suppose 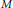$M$ is faithful over $R$, $R$ is a domain (we will show that we can restrict to this case without loss of generality), and 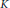$K$ is the quotient field of $R$. If 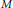$M$ is 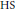$\text{HS}$ over 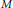$R$, then $R$ is 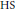$\text{HS}$ as a module over itself, 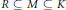$R\,\subseteq \,M\,\subseteq \,K$, and there exists a generating set $S$ for 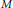$M$ over $R$ with 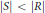$\left| S \right|\,<\,\left| R \right|$. We use this result to generalize a problem posed by Kaplansky and conclude the paper by answering an open question on Jónsson modules.

Keywords

13A9913C0513E0503E50Noetherian ringresidually finite ringcardinal numbercontinuum hypothesisvaluation ringJónsson module
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 2 , 01 June 2012 , pp. 378 - 389
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Chew, K. and Lawn, S., Residually finite rings. Canad. J. Math. 22(1970), 92–101. http://dx.doi.org/10.4153/CJM-1970-012-0 Google Scholar
[2] Coleman, E., Jonsson groups, rings, and algebras. Irish Math. Soc. Bull. No. 36 (1996), 34–45.Google Scholar
[3] Gilmer, R., Multiplicative Ideal Theory. Queen's Papers in Pure and Applied Mathematics 90. Queen's University, Kingston, ON, 1992.Google Scholar
[4] Gilmer, R. and Heinzer, W., An application of Jónsson modules to some questions concerning proper subrings. Math. Scand. 70(1992), no. 1, 34–42.Google Scholar
[5] Gilmer, R. and Heinzer, W., Cardinality of generating sets for ideals of a commutative ring. Indiana Univ. Math. J. 26(1977), no. 4, 791–798. http://dx.doi.org/10.1512/iumj.1977.26.26062 Google Scholar
[6] Gilmer, R. and Heinzer, W., Cardinality of generating sets for modules over a commutative ring. Math. Scand. 52(1983), no. 1, 41–57.Google Scholar
[7] Gilmer, R. and Heinzer, W., On Jónsson algebras over a commutative ring. J. Pure Appl. Algebra 49(1987), no. 1-2, 133–159. http://dx.doi.org/10.1016/S0022-4049(87)80009-9 Google Scholar
[8] Gilmer, R. and Heinzer, W., On Jónsson modules over a commutative ring. Acta Sci. Math. 46(1983), no. 1-4, 3–15.Google Scholar
[9] Jensen, B. A. and Miller, D. W., Commutative semigroups which are almost finite. Pacific J. Math. 27(1968), 533–538.Google Scholar
[10] Kaplansky, I., Infinite Abelian Groups. The University of Michigan Press, Ann Arbor, Michigan, 1954.Google Scholar
[11] Kearnes, K. and Oman, G., Cardinalities of residue fields of Noetherian integral domains. Comm. Algebra 38(2010), no. 10, 3580–3588. http://dx.doi.org/10.1080/00927870903200893 Google Scholar
[12] Levitz, K. and Mott, J., Rings with finite norm property. Canad. J. Math. 24(1972), 557–565. http://dx.doi.org/10.4153/CJM-1972-049-1 Google Scholar
[13] Oman, G., Jónsson modules over commutative rings. In: Commutative Rings: New Research. Nova Science Publishers, New York, 2009, pp. 1–6.Google Scholar
[14] Oman, G., Jónsson modules over Noetherian rings. Comm. Algebra 38(2010), no. 9, 3489–3498. http://dx.doi.org/10.1080/00927870902936943 Google Scholar
[15] Oman, G., Some results on Jónsson modules over a commutative ring. Houston J. Math. 35(2009), no. 1, 1–12.Google Scholar
[16] Orzech, M. and Ribes, L., Residual finiteness and the Hopft property in rings. J. Algebra 15(1970), 81–88. http://dx.doi.org/10.1016/0021-8693(70)90087-6 Google Scholar
[17] Tucci, R., Commutative semigroups whose proper homomorphic images are all of smaller cardinality. Kyungpook Math. J. 46 2006), no. 2, 231–233.Google Scholar
[18] Varadarajan, K., Residual finiteness in rings and modules. J. Ramanujan Math. Soc. 8(1993), no. 1-2, 29–48.Google Scholar