Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T19:36:05.819Z Has data issue: false hasContentIssue false
  • English
  • Français

On Non-Vanishing of Convolution of Dirichlet Series

Published online by Cambridge University Press:  20 November 2018

Amir Akbary  and
Shahab Shahabi
Amir Akbary
Affiliation:
Department of Mathematics and Computer Science, University of Lethbridge, 4401 University Drive West, Lethbridge, AB, T1K 3M4 e-mail: akbary@cs.uleth.ca
Shahab Shahabi
Affiliation:
Department of Mathematics and Statistics, McGill University, 805 SherbrookWest, Montreal, QC, H3A 2K6 e-mail: shahabi@math.mcgill.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the non-vanishing on the line 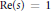$\operatorname{Re}\left( s \right)=1$ of the convolution series associated to two Dirichlet series in a certain class of Dirichlet series. The non-vanishing of various $L$-functions on the line 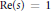$\operatorname{Re}\left( s \right)=1$ will be simple corollaries of our general theorems.

Keywords

11M41
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 3 , 01 September 2005 , pp. 321 - 332
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Davenport, H., Multiplicative Number Theory. Third ed. Graduate Texts in Mathematics 74, Springer-Verlag, New York, 2000.Google Scholar
[2] Ingham, A. E., Note on Riemann's ζ-function and Dirichlet's L-functions. J. London Math. Soc. 5(1930), 107–112.Google Scholar
[3] Jacquet, H. and Shalika, J. A., A non-vanishing theorem for zeta functions of GL n , Inventiones Math. 38(1976), 1–16.Google Scholar
[4] Koblitz, N., Introduction to elliptic curves and modular forms. Second ed. Springer-Verlag, New York, 1993.Google Scholar
[5] Murty, M. R., Problems in Analytic Number Theory. Graduate Texts in Mathematics 206, Springer-Verlag, New York, 2001.Google Scholar
[6] Murty, V. K., On the Sato-Tate conjecture. Prog. Math. 26(1982), 195–205.Google Scholar
[7] Narayanan, S., On the non-vanishing of a certain class of Dirichlet series. Canad. Math. Bull. 40(1997), 364–369.Google Scholar
[8] Ogg, A. P., On a convolution of L-series. Invent. Math. 7(1969), 297–312.Google Scholar
[9] Rankin, R. A., Contributions to the theory of Ramanujan's function τ (n) and similar arithmetical functions. I. Proc. Camb. Phil. Soc. 35(1939), 351–356.Google Scholar
[10] Rankin, R. A., Contributions to the theory of Ramanujan's function τ (n) and similar arithmetical functions. II. Proc. Camb. Phil. Soc. 35(1939), 357–372.Google Scholar
[11] Shahidi, F., On non-vanishing of L-functions, Bull. Amer.Math. Soc. (N.S.) 2(1980), 462–464.Google Scholar
[12] Shahidi, F., On non-vanishing of twisted symmetric and exterior square L-functions for GL(n), Pacific J. Math. 181(1997), 311–322.Google Scholar