Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-15T05:30:01.291Z Has data issue: false hasContentIssue false
  • English
  • Français

On Periodic Solutions of x‴ + ax″ + b′ + g(x) = 0

Published online by Cambridge University Press:  20 November 2018

R.R.D. Kemp
R.R.D. Kemp*
Affiliation:
Queen's University and Imperial College of Science and Technology
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [1] J. O. C. Ezeilo asks whether the equation

1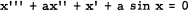

has periodic solutions for a ≠ 0. Since (1) has a two-dimensional space of solutions of period 2π if sin x is approximated by x, it is plausible to conclude, by analogy with x″ + sin x = 0, that (1) does have periodic solutions. However, when one applies the standard theory of perturbation of periodic solutions (treating a as small, see [2]), one finds that the only real periodic solutions obtainable in this manner are the trivial ones x(t, a) = nπ for some integer n.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 10 , Issue 1 , April 1967 , pp. 75 - 77
Copyright
Copyright © Canadian Mathematical Society 1967

Footnotes

1

This research was carried out while the author was partially supported by a grant from the Canada Council.

References

1. Ezeilo, J. O. C., Research Problem 12, Bull. Amer. Math. Soc. 72 (1966), page 470.Google Scholar
2. E.A. Coddington and Levinson, N., Theory of Ordinary Differential Equations. McGraw-Hill, New York (1955).Google Scholar