Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-15T06:55:02.771Z Has data issue: false hasContentIssue false
  • English
  • Français

On Point-Symmetric Tournaments

Published online by Cambridge University Press:  20 November 2018

Brian Alspach
Brian Alspach*
Affiliation:
Simon Fraser University, Burnaby, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

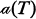A tournament is a directed graph in which there is exactly one arc between any two distinct vertices. Let denote the automorphism group of T. A tournament T is said to be point-symmetric if 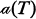acts transitively on the vertices of T. Let g(n) be the maximum value of 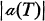taken over all tournaments of order n. In [3] Goldberg and Moon conjectured that 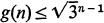with equality holding if and only if n is a power of 3. The case of point-symmetric tournaments is what prevented them from proving their conjecture. In [2] the conjecture was proved through the use of a lengthy combinatorial argument involving the structure of point-symmetric tournaments. The results in this paper are an outgrowth of an attempt to characterize point-symmetric tournaments so as to simplify the proof employed in [2].

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 3 , September 1970 , pp. 317 - 323
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Alspach, B., A class of tournaments, unpublished doctoral dissertation, University of California, Santa Barbara, 1966.Google Scholar
2. Alspach, B., A combinatorial proof of a conjecture of Goldberg and Moon, Canad. Math. Bull. 11 (1968), 655-661.Google Scholar
3. Goldberg, M. and Moon, J. W., On the maximum order of the group of a tournament, Canad. Math. Bull. 9 (1966), 563-569.Google Scholar
4. Moon, J. W., Tournaments with a given automorphism group, Canad. J. Math. 16 (1964) 485-489.Google Scholar
5. Rotman, J., The theory of groups: An introduction, Allyn and Bacon, Boston, 1966.Google Scholar
6. Turner, J., Point-symmetric graphs with a prime number of points, J. Comb. Theor. 3 (1967), 136-145.Google Scholar
7. Wielandt, H., Finite permutation groups, Trans. Bercov, R., Academic Press, New York, 1964.Google Scholar