No CrossRef data available.
Article contents
On Polarized K3 Surfaces of Genus 33
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We prove that the moduli space of smooth primitively polarized 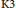 $\text{K3}$ surfaces of genus 33 is unirational.
$\text{K3}$ surfaces of genus 33 is unirational.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
[1]
Baily, W. L. and Borel, A., Compactification of arithmetic quotients of bounded symmetric domains.
Ann. of Math.
84(1966), 442–528. http://dx.doi.Org/10.2307/1970457
Google Scholar
[2]
Bogomolov, F. A. and Tschinkel, Yu., Density of rational points on elliptic K3 surfaces.
Asian J. Math.
4(2000), no. 2, 351–368. http://dx.doi.Org/10.4310/AJM.2000.v4.n2.a6
Google Scholar
[3]
Bourbaki, N., Elements of mathematics. Algebra I. Springer-Verlag, Berlion, 2007. Google Scholar
[4]
Dolgachev, I. V. and Kondo, S., Moduli spaces ofK3 surfaces and complex ball quotients. In: Arithmetic and geometry around hypergeometric functions, Prog. Math., 260, Birkhauser, Basel, 2007. pp. 43–100. http://dx.doi.Org/10.1007/978-3-7643-8284-1_3
Google Scholar
[5]
Friedman, R., Algebraic surfaces and holomorphic vector bundles. Universitext, Springer-Verlag, New York, 1998. http://dx.doi.Org/10.1007/978-1-4612-1688-9
Google Scholar
[6]
Griffiths, P. and Harris, J., Principles of algebraic geometry. Pure and Applied Mathematics, Wiley-Interscience, New York, 1978. Google Scholar
[7]
Gritsenko, V., Hulek, K., and Sankaran, G. K., The Kodaira dimension of the moduli ofK3 surfaces.
Invent. Math.
167(2007), 519–567. http://dx.doi.Org/10.1007/s00222-007-0054-1
Google Scholar
[8]
Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52, Springer-Verlag, New York-Heidelberg, 1977. Google Scholar
[9]
Iskovskikh, V. A. and Prokhorov, Yu. G., Fano varieties. Encyclopaedia of Mathematical Sciences, 47, Springer-Verlag, Berlin, 1999. Google Scholar
[10]
Karzhemanov, I., Fano threefolds with canonical Gorenstein singularities and big degree.
Math. Ann.
362(2015), no. 3-4, 1107–1142. http://dx.doi.Org/10.1007/s00208-014-1149-9
Google Scholar
[11]
Karzhemanov, I. V., On Fano threefolds with canonical Gorenstein singularities.
(Russian) Mat. Sb. 200(2009), no. 8,111-146; translation in Sb. Math. 200(2009), no. 7-8, 1215–1246. http://dx.doi.Org/10.4213/sm3946 http://dx.doi.org/10.1070/SM2009v200n08ABEH004035
Google Scholar
[12]
Karzhemanov, I., Remark on polarized K3 surfaces of genus 36.
Geom. Dedicata
59(2012), 295–305. http://dx.doi.Org/10.1007/s10711 -011-9660-6
Google Scholar
[13]
Kondo, S., On the Kodaira dimension of the moduli spaces o/K3 surfaces.
Compositio Math.
89(1993), no. 3, 251–299.Google Scholar
[14]
Kondo, S., On the Kodaira dimension of the moduli spaceso/K3 surfaces. II.
Compositio Math.
116(1999), no. 2, 111–117. http://dx.doi.Org/10.1023/A:1000675831026
Google Scholar
[15]
Mukai, S., Biregular classification of Fano threefolds and Fano manifolds ofcoindex
3. Proc. Nat. Acad. Sci. U.S.A.
86(1989), no. 9, 3000–3002. http://dx.doi.Org/1 0.1073/pnas.86.9.3000
Google Scholar
[16]
Mukai, S., Curves and K3 surfaces of genus eleven. In: Moduli of vector bundles (Sanda, 1994; Kyoto, 1994), Lecture Notes in Pure and Appl. Math., 179, Dekker, New York, 1996, pp. 189–197.Google Scholar
[17]
Mukai, S., Curves, K3 surfaces and Fano 3-folds of genus ^ 10. In: Algebraic geometry and commutative algebra, KinoKuniya, Tokyo, 1988, pp. 357–377.Google Scholar
[18]
Mukai, S., Fano 3-folds. In: Complex protective geometry (Trieste, 1989/Bergen, 1989), London Math. Soc. Lecture Note Ser., 179, Cambridge Univ. Press, Cambridge, 1992, pp. 255–263. http://dx.doi.Org/10.1017/CBO9780511662652.018
Google Scholar
[19]
Mukai, S., New developments in Fano manifold theory related to the vector bundle method and moduli problems.
(Japanese) Sugaku
47(1995), no. 2,125-144. Google Scholar
[20]
Mukai, S., On the moduli space of bundles on K3 surfaces. I. In: Vector bundles on algebraic varieties (Bombay, 1984), Tata Inst. Fund. Res. Stud. Math., 11, Tata Inst. Fund. Res., Bombay, 1987, pp 341–413.Google Scholar
[21]
Mukai, S., Polarized K3 surfaces of genus 18 and 20. In: Complex protective geometry (Trieste, 1989/Bergen, 1989), London Math. Soc. Lecture Note Ser., 179, Cambridge Univ. Press, Cambridge, 1992, pp. 264–276. http://dx.doi.Org/10.1017/CBO9780511662652.019
Google Scholar
[22]
Mukai, S., Polarized K3 surfaces of genus thirteen. In: Moduli spaces and arithmetic geometry, Adv. Stud. Pure Math., 45, Math. Soc. Japan, Tokyo, 2006, pp. 315–326.Google Scholar
[23]
Mukai, S., Symplectic structure of the moduli space of sheaves on an abelian or K3 surface.
Invent. Math.
77(1984), no. 1, 101–116. http://dx.doi.Org/10.1007/BF01389137
Google Scholar
[24]
Nikulin, V. V., Integral symmetric bilinear forms and some of their geometric applications.
(Russian) Izv. Akad. NaukSSSR Ser. Mat.
43(1979), no. 1,111-177, 238.Google Scholar
[25]
Nikulin, V. V., Finite automorphism groups ofKa'hler K3 surfaces.
Trans. Moscow Math. Soc.
38(1980), 71–135. Google Scholar
[26]
Saint-Donat, B., Protective models ofK - 3 surfaces.
Amer. J. Math.
96(1974), 602–639. http://dx.doi.Org/10.2307/2373709
Google Scholar
[27]
Viehweg, E., Quasi-Projective moduli for polarized manifolds. Ergebnisse der Mathematik und ihrer Grenzgebiete, 30, Springer-Verlag, Berlin, 1995. http://dx.doi.Org/10.1007/978-3-642-79745-3
Google Scholar


