Article contents
On Polynomials with Real Zeros
Published online by Cambridge University Press: 20 November 2018
Extract
Let
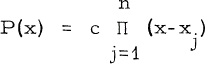
be a polynomial of degree n with real and non-negative zeros x1 ≤ x2 ≤ … xn. The zeros xj. will be said to have extent 1 if
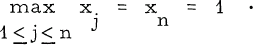
Let ξ1 ≤ ξ2 ≤ … ξn-1 be the zeros of the derived polynomial p'(x). The zeros ξ1, ξ2, …, ξn-1 are real and non-negative, and moreover their extent can be at most equal to the extent of the zeros x1, x2, …, xn. The two can indeed be equal. For if the extent of the zeros xj. is 1 and 1 is a multiple zero of p'(x) then ξn-1 = 1. However it is not quite clear how small ξn-1 = 1 can be if Xn = 1. The extent ξn-1 = 1. of the zeros of p'(x) is less than 1 only if 1 is not a multiple zero of p(x). So let us suppose that p(x) has a simple zero at x = 1. Consequently xn-1 is the largest zero of p(x)/(x-l) or equivalently the largest zero of p(x) in 0 < x < 1 and it follows by Rolle's theorem that p'(x) n as a zero in the interval (xn-1,1). Thus the extent ξn-1 of the zeros of p'(x) is greater than xn-1 and it remains to see how small it can be.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1968
References
- 1
- Cited by

