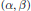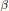Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yu, Changtao
and
Zhu, Hongmei
2011.
On a new class of Finsler metrics.
Differential Geometry and its Applications,
Vol. 29,
Issue. 2,
p.
244.
Xia, Qiaoling
2011.
On locally dually flat (α,β)-metrics.
Differential Geometry and its Applications,
Vol. 29,
Issue. 2,
p.
233.
Mo, Xiaohuan
2011.
On some projectively flat finsler metrics in terms of hypergeometric functions.
Israel Journal of Mathematics,
Vol. 184,
Issue. 1,
p.
59.
Li, Benling
and
Shen, Zhongmin
2012.
Projectively Flat Fourth Root Finsler Metrics.
Canadian Mathematical Bulletin,
Vol. 55,
Issue. 1,
p.
138.
YANG, GUOJUN
2013.
ON A CLASS OF SINGULAR PROJECTIVELY FLAT FINSLER METRICS WITH CONSTANT FLAG CURVATURE.
International Journal of Mathematics,
Vol. 24,
Issue. 10,
p.
1350087.
Binh, T. Q.
Kertész, D. Cs.
and
Tamássy, L.
2013.
On projectively flat Finsler spaces.
Acta Mathematica Hungarica,
Vol. 141,
Issue. 4,
p.
383.
Yang, Guojun
Mira, P.
and
Mokhov, O.
2013.
On a Class of Two‐Dimensional Douglas and Projectively Flat Finsler Metrics.
The Scientific World Journal,
Vol. 2013,
Issue. 1,
Yang, Guo Jun
2013.
On a class of two-dimensional projectively flat finsler metrics with constant flag curvature.
Acta Mathematica Sinica, English Series,
Vol. 29,
Issue. 5,
p.
959.
Chen, Guangzu
Cheng, Xinyue
and
Yuan, Mingao
2013.
On a class of projectively flat Finsler metrics with weakly isotropic flag curvature.
Periodica Mathematica Hungarica,
Vol. 67,
Issue. 2,
p.
155.
徐, 兵
2013.
Dually Flat Fourth Root Metric.
Pure Mathematics,
Vol. 03,
Issue. 03,
p.
195.
Yang, Guojun
2014.
On a class of singular Douglas and projectively flat Finsler metrics.
Differential Geometry and its Applications,
Vol. 32,
Issue. ,
p.
113.
Shen, Zhongmin
and
Yu, Changtao
2014.
On a class of Einstein Finsler metrics.
International Journal of Mathematics,
Vol. 25,
Issue. 04,
p.
1450030.
Mikeš, Josef
and
Stepanova, Elena
2014.
A five-dimensional Riemannian manifold with an irreducible SO(3)-structure as a model of abstract statistical manifold.
Annals of Global Analysis and Geometry,
Vol. 45,
Issue. 2,
p.
111.
Yu, Changtao
2014.
On dually flat(α,β)-metrics.
Journal of Mathematical Analysis and Applications,
Vol. 412,
Issue. 2,
p.
664.
Shen, Zhongmin
and
Yang, Guojun
2014.
On a class of weakly Einstein Finsler metrics.
Israel Journal of Mathematics,
Vol. 199,
Issue. 2,
p.
773.
Shen, Bin
2016.
Twisted Ricci flow on a class of Finsler metrics and its solitons.
Differential Geometry and its Applications,
Vol. 46,
Issue. ,
p.
132.
Liu, Wangfu
and
Li, Benling
2016.
Projectively flat Finsler metrics defined by the Euclidean metric and related 1-forms.
Differential Geometry and its Applications,
Vol. 46,
Issue. ,
p.
14.
Li, Benling
and
Shen, Zhongmin
2016.
On a class of locally projectively flat Finsler metrics.
International Journal of Mathematics,
Vol. 27,
Issue. 06,
p.
1650052.
Yu, Changtao
2016.
Deformations and Hilbert’s fourth problem.
Mathematische Annalen,
Vol. 365,
Issue. 3-4,
p.
1379.
Xia, Qiaoling
2016.
On a class of projectively flat Finsler metrics.
Differential Geometry and its Applications,
Vol. 44,
Issue. ,
p.
1.