Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-05T17:36:41.127Z Has data issue: false hasContentIssue false
  • English
  • Français

On Stanley Depths of Certain Monomial Factor Algebras

Published online by Cambridge University Press:  20 November 2018

Zhongming Tang
Zhongming Tang*
Affiliation:
Department of Mathematics, Suzhou University, Suzhou 215006, PR China. e-mail: zmtang@suda.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 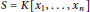$S\,=\,K\left[ {{x}_{1}},\,\ldots \,,\,{{x}_{n}} \right]$ be the polynomial ring in $n$-variables over a field 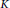$K$ and $I$ a monomial ideal of $S$. According to one standard primary decomposition of $I$, we get a Stanley decomposition of the monomial factor algebra 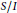$S/I$. Using this Stanley decomposition, one can estimate the Stanley depth of 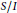$S/I$. It is proved that 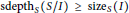$\text{sdept}{{\text{h}}_{s}}\left( S/I \right)\,\ge \,\text{siz}{{\text{e}}_{S}}\left( I \right)$. 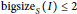When $I$ is squarefree and $\text{bigsiz}{{\text{e}}_{S}}\left( I \right)\,\le \,2$, the Stanley conjecture holds for 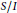$S/I$, i.e., 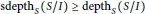$\text{sdept}{{\text{h}}_{S}}\left( S/I \right)\ge \text{dept}{{\text{h}}_{S}}\left( S/I \right)$.

Keywords

13F2013C15monomialideal sizeStanley depth
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 2 , 01 June 2015 , pp. 393 - 401
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Cimpoeas, C., Some remarks on the Stanley depth for multigraded modules. Matematiche (Catania) 63 (2008), no. 2,165–171.Google Scholar
[2] Herzog, J., Jahan, A. S., and X. Zheng, Skeletons of monomial ideals. Math. Nachr. 283 (2010), no. 10, 1403–1408. http://dx.doi.Org/10.1OO2/mana.2OO810039 Google Scholar
[3] Herzog, J., Popescu, D., and Vadoiu, M., Stanley depth and size of a monomial ideal. Proc. Amer. Math. Soc. 140 (2012), no. 2, 493–504. http://dx.doi.org/10.1090/S0002-9939-2011-11160-2 Google Scholar
[4] Ichim, B., Katthan, L., and Moyano-Fernandez, J. J., The behavior of Stanley depth under polarization. arxiv:1401.4309Google Scholar
[5] Lyubeznik, G., On the arithmetical rank of monomial ideals. J. Algebra, 112 (1988), no. 1, 86–89. http://dx.doi.Org/10.1016/0021-8693(88)90133–0 Google Scholar
[6] Popescu, A., Special Stanley decompositions. Bull. Math. Soc. Sci. Math. Roumanie 53 (101)(2010), no. 4, 363–372.Google Scholar
[7] Popescu, A., The Stanley conjecture on intersections of four monomial prime ideals. Comm. Algebra 41 (2013), no. 11,4351–4362. http://dx.doi.org/10.1080/00927872.2012.699568 Google Scholar
[8] Popescu, A., Graph and depth of a monomial squarefree ideal. Proc. Amer. Math. Soc. 140 (2012), no. 11, 3813–3822. http://dx.doi.org/10.1090/S0002–9939-2012-11371-1 Google Scholar
[9] Popescu, A., Stanley depth of multigraded modules. J. Algebra 321 (2009), no. 10, 2782–2797. http://dx.doi.Org/10.1016/j.jalgebra.2009.03.009 Google Scholar
[10] Popescu, D. and Qureshi, M. I., Computing the Stanley depth. J. Algebra 323 (2010), no. 10, 2943–2959. http://dx.doi.Org/10.1016/j.jalgebra.2009.11.025 Google Scholar
[11] Stanley, R. P., Linear Diophantine equations and local cohomology. Invent. Math. 68 (1982), no. 2, 175–193. http://dx.doi.org/10.1007/BF01394054 Google Scholar
[12] Tang, Z., Stanley depths of certain Stanley-Reisner rings. J. Algebra 409 (2014), 430–443. http://dx.doi.org/! 0.101 6/j.jalgebra.2O14.03.020 Google Scholar