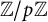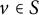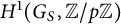1 Introduction
Let
![]() $D\in {\mathbb {Z}}$
be squarefree and odd and write
$D\in {\mathbb {Z}}$
be squarefree and odd and write
![]() $\infty |D$
if
$\infty |D$
if
![]() $D<0$
. It is well-known that there exists a quadratic extension
$D<0$
. It is well-known that there exists a quadratic extension
![]() $K/ {\mathbb Q}$
ramified at exactly the set of places
$K/ {\mathbb Q}$
ramified at exactly the set of places
![]() $\{v : v| D \}$
if and only if
$\{v : v| D \}$
if and only if
![]() $D\equiv 1$
mod
$D\equiv 1$
mod
![]() $4$
. The key is how the Frobenius elements of the
$4$
. The key is how the Frobenius elements of the
![]() $v|D$
lie in the Galois group of the governing extension
$v|D$
lie in the Galois group of the governing extension
![]() $ {\mathbb Q}(i)/ {\mathbb Q}$
. Let
$ {\mathbb Q}(i)/ {\mathbb Q}$
. Let
![]() $\sigma _v$
denote Frobenius at v in this extension with
$\sigma _v$
denote Frobenius at v in this extension with
![]() $\sigma _\infty $
being the nontrivial element of
$\sigma _\infty $
being the nontrivial element of
![]() $\mathrm{Gal}( {\mathbb Q}(i)/ {\mathbb Q})$
. We frame this result as the following Fact:
$\mathrm{Gal}( {\mathbb Q}(i)/ {\mathbb Q})$
. We frame this result as the following Fact:
Fact There exists a quadratic extension
![]() $K/ {\mathbb Q}$
ramified exactly at a tame (not containing
$K/ {\mathbb Q}$
ramified exactly at a tame (not containing
![]() $2$
but allowing
$2$
but allowing
![]() $\infty $
) set S of places if and only if
$\infty $
) set S of places if and only if
![]() $\displaystyle \sum _{v\in S} \sigma _v =0$
in
$\displaystyle \sum _{v\in S} \sigma _v =0$
in
![]() $\mathrm{Gal}( {\mathbb Q}(i)/ {\mathbb Q})$
.
$\mathrm{Gal}( {\mathbb Q}(i)/ {\mathbb Q})$
.
The paper [Reference Gras and MunnierGM] extended this to
![]() $ {\mathbb Z}/p{\mathbb Z} $
-extensions of a general number field K and, with some hypotheses, to
$ {\mathbb Z}/p{\mathbb Z} $
-extensions of a general number field K and, with some hypotheses, to
![]() ${\mathbb {Z}}/p^e{\mathbb {Z}}$
-extensions of K. To explain the result precisely, we need some background. For a fixed prime p and set S of tame places (prime to p and allowing real Archimedean places), let
${\mathbb {Z}}/p^e{\mathbb {Z}}$
-extensions of K. To explain the result precisely, we need some background. For a fixed prime p and set S of tame places (prime to p and allowing real Archimedean places), let
where J is a fractional ideal of K. Note
![]() $K^{\times p} \subset V_S$
for all S and
$K^{\times p} \subset V_S$
for all S and
![]() $S \subseteq T \implies V_T \subseteq V_S$
. Let
$S \subseteq T \implies V_T \subseteq V_S$
. Let
![]() ${\mathcal O}^{\times }_K$
and
${\mathcal O}^{\times }_K$
and
![]() $Cl_K[p]$
be, respectively, the units of K and the p-torsion in the class group of K. That
$Cl_K[p]$
be, respectively, the units of K and the p-torsion in the class group of K. That
![]() $V_\emptyset /K^{\times p}$
lies in the exact sequence
$V_\emptyset /K^{\times p}$
lies in the exact sequence
is well-known (see, e.g., Proposition 10.7.2 of [Reference Neukirch, Schmidt and WingbergNSW], though note that the definition of
![]() $V_\emptyset $
in [Reference Neukirch, Schmidt and WingbergNSW] is formulated slightly differently than the one used here, but they are easily shown to be equivalent. Click here for the updated online version
$V_\emptyset $
in [Reference Neukirch, Schmidt and WingbergNSW] is formulated slightly differently than the one used here, but they are easily shown to be equivalent. Click here for the updated online version
![]() $2.3$
). Set
$2.3$
). Set
![]() $K':=K(\mu _p)$
and
$K':=K(\mu _p)$
and
![]() $L:=K'(\sqrt [p]{V_\emptyset })$
. We call
$L:=K'(\sqrt [p]{V_\emptyset })$
. We call
![]() $L/K'$
the governing extension for K. When
$L/K'$
the governing extension for K. When
![]() $K= {\mathbb Q}$
and
$K= {\mathbb Q}$
and
![]() $p=2,$
one easily has
$p=2,$
one easily has
![]() $L= {\mathbb Q}(i)$
and we have recovered the field of the Fact.
$L= {\mathbb Q}(i)$
and we have recovered the field of the Fact.

As L is obtained by adjoining to
![]() $K'$
the pth roots of elements of K (not
$K'$
the pth roots of elements of K (not
![]() $K'$
), one easily shows that places
$K'$
), one easily shows that places
![]() $v^{\prime }_1,v^{\prime }_2$
of
$v^{\prime }_1,v^{\prime }_2$
of
![]() $K'$
above a fixed place v of K have Frobenius elements in
$K'$
above a fixed place v of K have Frobenius elements in
![]() $ \mathrm{Gal}(L/K')$
that differ by a nonzero scalar multiple. We abuse notation and for any
$ \mathrm{Gal}(L/K')$
that differ by a nonzero scalar multiple. We abuse notation and for any
![]() $v'$
of
$v'$
of
![]() $K'$
above v in K denote Frobenius at
$K'$
above v in K denote Frobenius at
![]() $v'$
by
$v'$
by
![]() $\sigma _v$
. The theorem of [Reference Gras and MunnierGM] (also see Chapter V of [Reference GrasG]) below and Theorem 1.1 implicitly use this abuse of notation.
$\sigma _v$
. The theorem of [Reference Gras and MunnierGM] (also see Chapter V of [Reference GrasG]) below and Theorem 1.1 implicitly use this abuse of notation.
Theorem (Gras–Munnier)
Let p be a prime, and let S be a finite set of tame places (prime to p and allowing real Archimedean places if
![]() $p=2$
) of K. For
$p=2$
) of K. For
![]() $v \in S$
finite, we require that
$v \in S$
finite, we require that
![]() $N(v) \equiv 1$
mod p. There exists a
$N(v) \equiv 1$
mod p. There exists a
![]() ${\mathbb {Z}}/p{\mathbb {Z}}$
-extension of K ramified at exactly the places of S if and only if there exists a dependence relation
${\mathbb {Z}}/p{\mathbb {Z}}$
-extension of K ramified at exactly the places of S if and only if there exists a dependence relation
![]() $\displaystyle \sum _{v\in S} a_v \sigma _v =0$
with all
$\displaystyle \sum _{v\in S} a_v \sigma _v =0$
with all
![]() $a_v \neq 0$
in the
$a_v \neq 0$
in the
![]() $ {\mathbb F} _p$
-vector space
$ {\mathbb F} _p$
-vector space
![]() $\mathrm{Gal}(L/K')$
.
$\mathrm{Gal}(L/K')$
.
Theorem 1.1 is a generalization of the Gras–Munnier Theorem. We first give a short proof that uses only one element of class field theory, the Koch–Shafarevich formula (2.1). We easily prove Proposition 2.2 from (2.1), after which one only needs a standard inclusion–exclusion argument to prove Theorem 1.1. The cardinalities of the two sets of Theorem 1.1 being equal suggests a duality. In the final section of this note, we give an alternative proof of Proposition 2.2 using the Greenberg–Wiles formula whose proof requires the full strength of global duality. Denote by
![]() $G_S$
, the Galois group over K of its maximal pro-p extension unramified outside S and recall that for
$G_S$
, the Galois group over K of its maximal pro-p extension unramified outside S and recall that for
![]() $0 \neq f \in H^1(G_S,{\mathbb {Z}}/p{\mathbb {Z}})=\mathrm{Hom}(G_S,{\mathbb {Z}}/p{\mathbb {Z}})$
,
$0 \neq f \in H^1(G_S,{\mathbb {Z}}/p{\mathbb {Z}})=\mathrm{Hom}(G_S,{\mathbb {Z}}/p{\mathbb {Z}})$
,
![]() $\mbox {Kernel}(f)$
fixes a
$\mbox {Kernel}(f)$
fixes a
![]() $ {\mathbb Z}/p{\mathbb Z} $
-extension of
$ {\mathbb Z}/p{\mathbb Z} $
-extension of
![]() $K_f/K$
unramified outside S. Our main result is the following theorem.
$K_f/K$
unramified outside S. Our main result is the following theorem.
Theorem 1.1 Let p be a prime, and let S be a finite set of tame places (prime to p and allowing real Archimedean places if
![]() $p=2$
) of a number field K where we require
$p=2$
) of a number field K where we require
![]() $N(v) \equiv 1$
mod p. The sets below have the same cardinality:
$N(v) \equiv 1$
mod p. The sets below have the same cardinality:
 $$ \begin{align*}\left\{ f\in \frac{H^1(G_S, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )} \,\mid \, \mbox{ the extension } K_f/K \mbox{ is ramified exactly at the places of } S\right\}\end{align*} $$
$$ \begin{align*}\left\{ f\in \frac{H^1(G_S, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )} \,\mid \, \mbox{ the extension } K_f/K \mbox{ is ramified exactly at the places of } S\right\}\end{align*} $$
and
 $$ \begin{align*}\bigg\{\mbox{Dependence relations }\sum_{v\in S} a_v\sigma_v=0 \mbox{ with all } a_v\neq 0 \mbox{ in }\mathrm{Gal}(L/K')\bigg\}.\end{align*} $$
$$ \begin{align*}\bigg\{\mbox{Dependence relations }\sum_{v\in S} a_v\sigma_v=0 \mbox{ with all } a_v\neq 0 \mbox{ in }\mathrm{Gal}(L/K')\bigg\}.\end{align*} $$
When
![]() $p=2$
, there is clearly at most one dependence relation. If
$p=2$
, there is clearly at most one dependence relation. If
![]() $K(\sqrt {\alpha _1})$
and
$K(\sqrt {\alpha _1})$
and
![]() $K(\sqrt {\alpha _2})$
are both ramified at all
$K(\sqrt {\alpha _2})$
are both ramified at all
![]() $v \in S$
, the “diagonal” extension
$v \in S$
, the “diagonal” extension
![]() $K(\sqrt {\alpha _1\alpha _2})$
is unramified everywhere, so there is a unique
$K(\sqrt {\alpha _1\alpha _2})$
is unramified everywhere, so there is a unique
 $f \in \displaystyle \frac {H^1(G_S,{\mathbb {Z}}/2{\mathbb {Z}})}{H^1(G_\emptyset ,{\mathbb {Z}}/2{\mathbb {Z}})}$
giving rise to the ramified extension and the bijection is natural in this case.
$f \in \displaystyle \frac {H^1(G_S,{\mathbb {Z}}/2{\mathbb {Z}})}{H^1(G_\emptyset ,{\mathbb {Z}}/2{\mathbb {Z}})}$
giving rise to the ramified extension and the bijection is natural in this case.
For examples and applications, we refer the reader to [Reference Hajir, Maire and RamakrishnaHMR], especially the examples in Section 3. Note that
![]() $p=2$
in those examples and the primes of S all have trivial Frobenius element in the governing extension.
$p=2$
in those examples and the primes of S all have trivial Frobenius element in the governing extension.
2 Proof of Theorem 1.1
For any field E, set
 $\delta (E) = \left \{\hspace{-4pt}\begin{array}{cc} 1, & \mu _p \subset E,\\0, &\mu _p \not \subset E. \end {array} \right. $
Dirichlet’s unit theorem and (1.1) imply
$\delta (E) = \left \{\hspace{-4pt}\begin{array}{cc} 1, & \mu _p \subset E,\\0, &\mu _p \not \subset E. \end {array} \right. $
Dirichlet’s unit theorem and (1.1) imply
![]() $\mathrm{Gal}(L/K')$
is an
$\mathrm{Gal}(L/K')$
is an
![]() $ {\mathbb F} _p$
-vector space of dimension
$ {\mathbb F} _p$
-vector space of dimension
![]() $r_1+r_2-1+\delta (K)+ \dim Cl_K[p]$
, where
$r_1+r_2-1+\delta (K)+ \dim Cl_K[p]$
, where
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are the number of real and pairs of complex embeddings of K. The standard fact from class field theory that we need (see [Reference KochK, Section 11.3] or [Reference Neukirch, Schmidt and WingbergNSW, Section 10.7]) is a formula of Koch and Shafarevich for the dimension of the space of
$r_2$
are the number of real and pairs of complex embeddings of K. The standard fact from class field theory that we need (see [Reference KochK, Section 11.3] or [Reference Neukirch, Schmidt and WingbergNSW, Section 10.7]) is a formula of Koch and Shafarevich for the dimension of the space of
![]() $ {\mathbb Z}/p{\mathbb Z} $
-extensions of K unramified outside a tame (prime to p and allowing real Archimedean places if
$ {\mathbb Z}/p{\mathbb Z} $
-extensions of K unramified outside a tame (prime to p and allowing real Archimedean places if
![]() $p=2$
) set Z:
$p=2$
) set Z:
 $$ \begin{align} \dim H^1(G_Z, {\mathbb Z}/p{\mathbb Z} ) =-r_1-r_2+1-\delta(K) + \dim (V_Z/K^{\times p}) + \left(\sum_{v \in Z} \delta(K_v) \right). \end{align} $$
$$ \begin{align} \dim H^1(G_Z, {\mathbb Z}/p{\mathbb Z} ) =-r_1-r_2+1-\delta(K) + \dim (V_Z/K^{\times p}) + \left(\sum_{v \in Z} \delta(K_v) \right). \end{align} $$
Fix a tame set S noting that
![]() $H^1(G_S, {\mathbb Z}/p{\mathbb Z} )$
may include cohomology classes that cut out
$H^1(G_S, {\mathbb Z}/p{\mathbb Z} )$
may include cohomology classes that cut out
![]() $ {\mathbb Z}/p{\mathbb Z} $
-extensions of K that could be ramified at proper subsets of S. As we vary Z from
$ {\mathbb Z}/p{\mathbb Z} $
-extensions of K that could be ramified at proper subsets of S. As we vary Z from
![]() $\emptyset $
to S one place at a time,
$\emptyset $
to S one place at a time,
![]() $\dim (V_Z/K^{\times p})$
may remain the same or decrease by
$\dim (V_Z/K^{\times p})$
may remain the same or decrease by
![]() $1$
. Since
$1$
. Since
![]() $\delta (K_v)=1$
, we see
$\delta (K_v)=1$
, we see
![]() $\dim H^1(G_Z, {\mathbb Z}/p{\mathbb Z} )$
increases by
$\dim H^1(G_Z, {\mathbb Z}/p{\mathbb Z} )$
increases by
![]() $1$
or remains the same, respectively.
$1$
or remains the same, respectively.
Let
![]() $W \subset \mathrm{Gal}(L/K')$
be the
$W \subset \mathrm{Gal}(L/K')$
be the
![]() $ {\mathbb F} _p$
-subspace spanned by
$ {\mathbb F} _p$
-subspace spanned by
![]() $\langle \sigma _v\rangle _{v\in S}$
, the Frobenius elements of the places in S. Recall that each
$\langle \sigma _v\rangle _{v\in S}$
, the Frobenius elements of the places in S. Recall that each
![]() $\sigma _v$
is well-defined up to a nonzero scalar multiple so W is well-defined. Let
$\sigma _v$
is well-defined up to a nonzero scalar multiple so W is well-defined. Let
![]() $I:= \{u_1,u_2,\ldots ,u_r\} \subset S$
be such that
$I:= \{u_1,u_2,\ldots ,u_r\} \subset S$
be such that
![]() $\{\sigma _{u_1},\sigma _{u_2},\ldots ,\sigma _{u_r} \}$
form a basis of W, and let
$\{\sigma _{u_1},\sigma _{u_2},\ldots ,\sigma _{u_r} \}$
form a basis of W, and let
![]() $D:=\{ w_1,w_2,\ldots ,w_s\} \subset S$
be the remaining elements of S. We think of the
$D:=\{ w_1,w_2,\ldots ,w_s\} \subset S$
be the remaining elements of S. We think of the
![]() $\sigma _{u_i}$
as independent elements and the
$\sigma _{u_i}$
as independent elements and the
![]() $\sigma _{w_j}$
as the dependent elements. Recall
$\sigma _{w_j}$
as the dependent elements. Recall
![]() $L:=K'(\sqrt [p]{V_\emptyset })$
so
$L:=K'(\sqrt [p]{V_\emptyset })$
so
![]() $\mathrm{Gal}(L/K')$
is dual to
$\mathrm{Gal}(L/K')$
is dual to
![]() $V_\emptyset /K^{\times p}$
, so as we vary Z in (2.1) from
$V_\emptyset /K^{\times p}$
, so as we vary Z in (2.1) from
![]() $\emptyset $
to I by adding in one
$\emptyset $
to I by adding in one
![]() $u_i$
at a time, we are adding
$u_i$
at a time, we are adding
![]() $1$
through the
$1$
through the
![]() $\delta (K_{u_i})$
term to the right side, but
$\delta (K_{u_i})$
term to the right side, but
![]() $\dim V_Z/K^{\times p}$
becomes one dimension smaller. Thus, both sides remain unchanged. Then, as we add in the dependent places
$\dim V_Z/K^{\times p}$
becomes one dimension smaller. Thus, both sides remain unchanged. Then, as we add in the dependent places
![]() $w_j$
of D to get to
$w_j$
of D to get to
![]() $S=I\cup D$
, we are not changing the span of the Frobenius elements so we have
$S=I\cup D$
, we are not changing the span of the Frobenius elements so we have
![]() $V_I/K^{\times p} = V_S/K^{\times p}$
. Thus
$V_I/K^{\times p} = V_S/K^{\times p}$
. Thus
 $$ \begin{align} H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} ) = H^1(G_I, {\mathbb Z}/p{\mathbb Z} ) \mbox{ and } \dim \left(\frac{H^1(G_S, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )}\right)=s. \end{align} $$
$$ \begin{align} H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} ) = H^1(G_I, {\mathbb Z}/p{\mathbb Z} ) \mbox{ and } \dim \left(\frac{H^1(G_S, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )}\right)=s. \end{align} $$
We write each
![]() $\sigma _{w_j}$
uniquely as a linear combination of the
$\sigma _{w_j}$
uniquely as a linear combination of the
![]() $\sigma _{u_i}$
:
$\sigma _{u_i}$
:
 $$ \begin{align*}R_j:\,\, \sigma_{w_j} - \sum^r_{i=1} F_{ji} \sigma_{u_i}=0.\end{align*} $$
$$ \begin{align*}R_j:\,\, \sigma_{w_j} - \sum^r_{i=1} F_{ji} \sigma_{u_i}=0.\end{align*} $$
For
![]() $X\subseteq S$
, let
$X\subseteq S$
, let
![]() $R_X$
be the
$R_X$
be the
![]() $ {\mathbb F} _p$
-vector space of all dependence relations on the elements
$ {\mathbb F} _p$
-vector space of all dependence relations on the elements
![]() $\{\sigma _v\}_{v\in X} \subset \mathrm{Gal}(L/K')$
.
$\{\sigma _v\}_{v\in X} \subset \mathrm{Gal}(L/K')$
.
Lemma 2.1 The set
![]() $\{R_1,R_2,\ldots ,R_s\}$
forms a basis of the
$\{R_1,R_2,\ldots ,R_s\}$
forms a basis of the
![]() $ {\mathbb F} _p$
-vector space of
$ {\mathbb F} _p$
-vector space of
![]() $R_S$
.
$R_S$
.
Proof Clearly,
![]() $\{R_j\}_{j=1,\dots ,s}$
is independent. We show they span
$\{R_j\}_{j=1,\dots ,s}$
is independent. We show they span
![]() $R_{{S}}$
. Consider any dependence relation
$R_{{S}}$
. Consider any dependence relation
![]() $R \in R_{{S}}$
. We can eliminate any
$R \in R_{{S}}$
. We can eliminate any
![]() $\sigma _{w_j}$
term in R by adding a suitable multiple of
$\sigma _{w_j}$
term in R by adding a suitable multiple of
![]() $R_j$
. We are left with a dependence relation on the
$R_j$
. We are left with a dependence relation on the
![]() $\sigma _{u_i}$
, which are independent, so it is trivial.
$\sigma _{u_i}$
, which are independent, so it is trivial.
Proposition 2.2 For any
![]() $X \subseteq S$
,
$X \subseteq S$
,
 $\displaystyle \dim R_X = \dim \left ( \frac {H^1(G_X, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset , {\mathbb Z}/p{\mathbb Z} )}\right ).$
$\displaystyle \dim R_X = \dim \left ( \frac {H^1(G_X, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset , {\mathbb Z}/p{\mathbb Z} )}\right ).$
Proof Lemma 2.1 and (2.2) prove this for
![]() $X=S$
. For
$X=S$
. For
![]() $X \subset S$
, let
$X \subset S$
, let
![]() $W_X \subset \mathrm{Gal}(L/K') $
be the span of the Frobenius elements of X. Form
$W_X \subset \mathrm{Gal}(L/K') $
be the span of the Frobenius elements of X. Form
![]() $I_X$
and
$I_X$
and
![]() $D_X$
as we formed I and D above and apply the proof above with X,
$D_X$
as we formed I and D above and apply the proof above with X,
![]() $I_X$
and
$I_X$
and
![]() $D_X$
playing the roles of S, I and D.
$D_X$
playing the roles of S, I and D.
Proposition 2.2 does not complete the proof of Theorem 1.1 as
![]() $R_S$
may contain dependence relations with support properly contained in S and
$R_S$
may contain dependence relations with support properly contained in S and
 $\displaystyle \frac {H^1(G_S, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset , {\mathbb Z}/p{\mathbb Z} )}$
may contain elements giving rise to extensions of K ramified at proper subsets of S.
$\displaystyle \frac {H^1(G_S, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset , {\mathbb Z}/p{\mathbb Z} )}$
may contain elements giving rise to extensions of K ramified at proper subsets of S.
Proof of Theorem 1.1
The set of dependence relations with support exactly in S is
those with support contained in S less the union of those with proper maximal support in S. For any sets
![]() $A_i \subset S$
, it is clear that
$A_i \subset S$
, it is clear that
![]() $\bigcap R_{A_i} = R_{\bigcap A_i},$
so by inclusion–exclusion,
$\bigcap R_{A_i} = R_{\bigcap A_i},$
so by inclusion–exclusion,
Similarly, the set of cohomology classes giving rise to
![]() ${\mathbb {Z}}/p{\mathbb {Z}}$
-extensions ramified exactly at the places of S (up to unramified extensions) is
${\mathbb {Z}}/p{\mathbb {Z}}$
-extensions ramified exactly at the places of S (up to unramified extensions) is
 $$ \begin{align} \frac{H^1(G_{S}, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )} \backslash \bigcup_{v\in S} \frac{ H^1(G_{ S\backslash \{v\} }, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )}. \end{align} $$
$$ \begin{align} \frac{H^1(G_{S}, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )} \backslash \bigcup_{v\in S} \frac{ H^1(G_{ S\backslash \{v\} }, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )}. \end{align} $$
Since, for any sets
![]() $A_i \subset S$
, we have
$A_i \subset S$
, we have
 $$ \begin{align*}\bigcap \frac{H^1(G_{A_i}, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )} =\frac{ H^1(G_{ \cap A_i}, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )},\end{align*} $$
$$ \begin{align*}\bigcap \frac{H^1(G_{A_i}, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )} =\frac{ H^1(G_{ \cap A_i}, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )},\end{align*} $$
we see
 $$ \begin{align} \# \bigcup_{v\in S} \frac{ H^1(G_{ S\backslash \{v\} }, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )} = \sum_{v\in S} \# \frac{ H^1(G_{ S\backslash \{v\} }, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )} - \sum_{v\neq w \in S} \# \frac{ H^1(G_{ S\backslash \{v,w\} }, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )} + \cdots. \end{align} $$
$$ \begin{align} \# \bigcup_{v\in S} \frac{ H^1(G_{ S\backslash \{v\} }, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )} = \sum_{v\in S} \# \frac{ H^1(G_{ S\backslash \{v\} }, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )} - \sum_{v\neq w \in S} \# \frac{ H^1(G_{ S\backslash \{v,w\} }, {\mathbb Z}/p{\mathbb Z} )}{H^1(G_\emptyset, {\mathbb Z}/p{\mathbb Z} )} + \cdots. \end{align} $$
Proposition 2.2 implies the terms on the right sides of (2.4) and (2.6) are equal so the left sides are equal as well. The theorem follows from (2.3), (2.5) and applying Proposition 2.2 with
![]() $X=S$
.
$X=S$
.
3 A proof via the Greenberg–Wiles formula
As the association of dependence relations and cohomology classes in Theorem 1.1 resembles a duality result, we reprove Proposition 2.2 using the Greenberg–Wiles formula, which follows from global duality. We assume familiarity with local and global Galois cohomology.
Henceforth, we assume the hypothesis of the Greenberg–Wiles formula that Z is a set of places of K containing all those above
![]() $\{p,\infty \}$
. For each
$\{p,\infty \}$
. For each
![]() $v\in Z$
, let
$v\in Z$
, let
![]() $G_v:=\mathrm{Gal}(\bar {K}_v/K_v)$
, where
$G_v:=\mathrm{Gal}(\bar {K}_v/K_v)$
, where
![]() $\bar {K}_v$
is an algebraic closure of
$\bar {K}_v$
is an algebraic closure of
![]() $K_v$
, and consider a subspace
$K_v$
, and consider a subspace
![]() $L_v \subseteq H^1(G_v,{\mathbb {Z}}/p{\mathbb {Z}})$
. Under the perfect local duality pairing (see [Reference Neukirch, Schmidt and WingbergNSW, Chapter 7, Section 2]),
$L_v \subseteq H^1(G_v,{\mathbb {Z}}/p{\mathbb {Z}})$
. Under the perfect local duality pairing (see [Reference Neukirch, Schmidt and WingbergNSW, Chapter 7, Section 2]),
![]() $L_v$
has an annihilator
$L_v$
has an annihilator
![]() $L^\perp _v \subseteq H^1(G_v,\mu _p)$
. Set
$L^\perp _v \subseteq H^1(G_v,\mu _p)$
. Set
 $$ \begin{align*}H^1_{\mathcal L}(G_Z,{\mathbb{Z}} / p{\mathbb{Z}}) := \mbox{Kernel} \left( H^1(G_Z,{\mathbb{Z}} / p{\mathbb{Z}}) \to \oplus_{v\in Z} \frac{H^1(G_v, { {\mathbb Z}/p{\mathbb Z}})}{L_v}\right)\end{align*} $$
$$ \begin{align*}H^1_{\mathcal L}(G_Z,{\mathbb{Z}} / p{\mathbb{Z}}) := \mbox{Kernel} \left( H^1(G_Z,{\mathbb{Z}} / p{\mathbb{Z}}) \to \oplus_{v\in Z} \frac{H^1(G_v, { {\mathbb Z}/p{\mathbb Z}})}{L_v}\right)\end{align*} $$
and
 $$ \begin{align*}H^1_{{\mathcal L}^\perp}(G_Z,\mu_p) := \mbox{Kernel} \left( H^1(G_Z,\mu_p) \to \oplus_{v\in Z} \frac{H^1(G_v,\mu_p)}{L^\perp_v}\right).\end{align*} $$
$$ \begin{align*}H^1_{{\mathcal L}^\perp}(G_Z,\mu_p) := \mbox{Kernel} \left( H^1(G_Z,\mu_p) \to \oplus_{v\in Z} \frac{H^1(G_v,\mu_p)}{L^\perp_v}\right).\end{align*} $$
We call
![]() $\{L_v\}_{v \in Z}$
and
$\{L_v\}_{v \in Z}$
and
![]() $\{ L^\perp _v \}_{v\in Z}$
the Selmer and dual Selmer conditions and
$\{ L^\perp _v \}_{v\in Z}$
the Selmer and dual Selmer conditions and
![]() $H^1_{\mathcal L}(G_Z,{\mathbb {Z}} / p{\mathbb {Z}})$
and
$H^1_{\mathcal L}(G_Z,{\mathbb {Z}} / p{\mathbb {Z}})$
and
![]() $H^1_{{\mathcal L}^\perp }(G_Z,\mu _p)$
the Selmer and dual Selmer groups.
$H^1_{{\mathcal L}^\perp }(G_Z,\mu _p)$
the Selmer and dual Selmer groups.
We need Lemma 3.1 and the Greenberg–Wiles formula below for our second proof of Proposition 2.2. As Lemma 3.1(ii) is perhaps not so well-known, we include a sketch of its proof.
Lemma 3.1
-
(i) For
 $v\nmid p$
, the unramified cohomology classes
$v\nmid p$
, the unramified cohomology classes
 $H_{nr}^1(G_v,{\mathbb {Z}}/p{\mathbb {Z}})$
and
$H_{nr}^1(G_v,{\mathbb {Z}}/p{\mathbb {Z}})$
and
 $H_{nr}^1(G_v,\mu _p)$
are exact annihilators of one another under the local duality pairing.
$H_{nr}^1(G_v,\mu _p)$
are exact annihilators of one another under the local duality pairing. -
(ii) Suppose
 $v|p$
and set
$v|p$
and set
 $K^{\prime }_v=K_v(\mu _p)$
. The annihilator of
$K^{\prime }_v=K_v(\mu _p)$
. The annihilator of
 $H_{nr}^1(G_v,{\mathbb {Z}}/p{\mathbb {Z}}) \subset H^1(G_v,{\mathbb {Z}}/p{\mathbb {Z}})$
is
$H_{nr}^1(G_v,{\mathbb {Z}}/p{\mathbb {Z}}) \subset H^1(G_v,{\mathbb {Z}}/p{\mathbb {Z}})$
is
 $H^1_f(G_v,\mu _p) \subset H^1(G_v,\mu _p)$
, the peu ramifiée classes, namely, those
$H^1_f(G_v,\mu _p) \subset H^1(G_v,\mu _p)$
, the peu ramifiée classes, namely, those
 $f\in {H^1(G_v,\mu _p)}$
whose fixed field
$f\in {H^1(G_v,\mu _p)}$
whose fixed field
 $L_{v,f}$
of Kernel
$L_{v,f}$
of Kernel
 $(f |_{G_{K^{\prime }_v}})$
arises from adjoining the pth root of a unit
$(f |_{G_{K^{\prime }_v}})$
arises from adjoining the pth root of a unit
 $u_f \in K_v$
.
$u_f \in K_v$
.
Proof
-
(i) This is standard (see [Reference Neukirch, Schmidt and WingbergNSW, Theorem 7.2.15]).
-
(ii) This result is Corollary 1.4 in Chapter III of [Reference MilneM], but we sketch the proof.
It follows once we explain the commutative diagram below.

Cohomology taken over
![]() $\mathrm{Spec}({\mathcal O}_{K_v})$
is flat. The rows are cup product pairings in flat and Galois cohomology. Recall
$\mathrm{Spec}({\mathcal O}_{K_v})$
is flat. The rows are cup product pairings in flat and Galois cohomology. Recall
![]() $ { {\mathbb Z}/p{\mathbb Z}} \simeq H^1_{nr}(G_v, { {\mathbb Z}/p{\mathbb Z}}) = H^1(\mathrm{Spec}({\mathcal O}_{K_v}), { {\mathbb Z}/p{\mathbb Z}}) \subset H^1(G_v, { {\mathbb Z}/p{\mathbb Z}})$
and
$ { {\mathbb Z}/p{\mathbb Z}} \simeq H^1_{nr}(G_v, { {\mathbb Z}/p{\mathbb Z}}) = H^1(\mathrm{Spec}({\mathcal O}_{K_v}), { {\mathbb Z}/p{\mathbb Z}}) \subset H^1(G_v, { {\mathbb Z}/p{\mathbb Z}})$
and
where the containment is codimension one as
![]() $ {\mathbb F}_p$
-vector spaces. Lemma 1.1 in Chapter III of [Reference MilneM] gives the two left vertical injections and the triviality of the top pairing. This last pairing is consistent with the local duality pairing of the bottom row of the above diagram. As
$ {\mathbb F}_p$
-vector spaces. Lemma 1.1 in Chapter III of [Reference MilneM] gives the two left vertical injections and the triviality of the top pairing. This last pairing is consistent with the local duality pairing of the bottom row of the above diagram. As
![]() $H^1_{nr}(G_v, { {\mathbb Z}/p{\mathbb Z}}) \subset H^1(G_v, { {\mathbb Z}/p{\mathbb Z}}) $
and
$H^1_{nr}(G_v, { {\mathbb Z}/p{\mathbb Z}}) \subset H^1(G_v, { {\mathbb Z}/p{\mathbb Z}}) $
and
![]() $H^1_f(G_v,\mu _p) \subset H^1(G_v,\mu _p)$
are dimension
$H^1_f(G_v,\mu _p) \subset H^1(G_v,\mu _p)$
are dimension
![]() $1$
and codimension
$1$
and codimension
![]() $1,$
respectively, they are exact annihilators of one another, proving (ii).
$1,$
respectively, they are exact annihilators of one another, proving (ii).
Theorem (Greenberg–Wiles)
Assume Z contains all places above
![]() $\{p,\infty \}$
. Then
$\{p,\infty \}$
. Then
 $$ \begin{align*} \begin{array}{ll} \dim H^1_{\mathcal L}(G_Z,{\mathbb{Z}} / p{\mathbb{Z}}) - \dim H^1_{{\mathcal L}^\perp}(G_Z,\mu_p) =& \\ \dim H^0(G_Z,{\mathbb{Z}}/p{\mathbb{Z}}) - \dim H^0(G_Z,\mu_p) + \sum_{v\in Z} \left(\dim L_v - \dim H^0(G_v,{\mathbb{Z}}/p{\mathbb{Z}}) \right). & \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \dim H^1_{\mathcal L}(G_Z,{\mathbb{Z}} / p{\mathbb{Z}}) - \dim H^1_{{\mathcal L}^\perp}(G_Z,\mu_p) =& \\ \dim H^0(G_Z,{\mathbb{Z}}/p{\mathbb{Z}}) - \dim H^0(G_Z,\mu_p) + \sum_{v\in Z} \left(\dim L_v - \dim H^0(G_v,{\mathbb{Z}}/p{\mathbb{Z}}) \right). & \end{array} \end{align*} $$
See Theorem
![]() $8.7.9$
of [Reference Neukirch, Schmidt and WingbergNSW] for a proof.
$8.7.9$
of [Reference Neukirch, Schmidt and WingbergNSW] for a proof.
Second proof of Proposition 2.2
Recall X is tame and write
![]() $X:=X_{<\infty } \cup X_\infty $
. Set
$X:=X_{<\infty } \cup X_\infty $
. Set
![]() $Z:= Z_p \cup X_{<\infty } \cup Z_\infty $
, where
$Z:= Z_p \cup X_{<\infty } \cup Z_\infty $
, where
![]() $Z_p:= \{v : v|p\}$
and
$Z_p:= \{v : v|p\}$
and
![]() $Z_\infty $
is the set of all real Archimedean places of K (so
$Z_\infty $
is the set of all real Archimedean places of K (so
![]() $X_\infty \subseteq Z_\infty $
).
$X_\infty \subseteq Z_\infty $
).
For v complex Archimedean, we have
![]() $G_v=\{e\}$
so the Selmer and dual Selmer conditions are trivial. For v real Archimedean,
$G_v=\{e\}$
so the Selmer and dual Selmer conditions are trivial. For v real Archimedean,
![]() $\dim H^1(G_v,{\mathbb {Z}}/2{\mathbb {Z}}) = \dim H^1(G_v,\mu _2)=1$
and the pairing between them is perfect (see Chapter I, Theorem
$\dim H^1(G_v,{\mathbb {Z}}/2{\mathbb {Z}}) = \dim H^1(G_v,\mu _2)=1$
and the pairing between them is perfect (see Chapter I, Theorem
![]() $2.13$
of [Reference MilneM, Chapter I, Theorem 2.13]). It is easy to see in this case that the unramified cohomology groups are trivial.
$2.13$
of [Reference MilneM, Chapter I, Theorem 2.13]). It is easy to see in this case that the unramified cohomology groups are trivial.
In the table below, we choose
![]() $\{M_v\}_{v\in Z}$
and
$\{M_v\}_{v\in Z}$
and
![]() $\{N_v\}_{v\in Z}$
so that
$\{N_v\}_{v\in Z}$
so that
The previous paragraph and Lemma 3.1 justify the stated dual Selmer conditions of the table.
 $$ \begin{align*} \begin{array}{l|cccc} & M_v & M^\perp_v & N_v & N^\perp_v \\ \hline\\[-9pt] v\in Z_p & H^1_{nr}(G_v,{\mathbb{Z}}/p{\mathbb{Z}}) & H^1_{f}(G_v,\mu_p) & H^1_{nr}(G_v,{\mathbb{Z}}/p{\mathbb{Z}}) & H^1_{f}(G_v,\mu_p) \\ v\in X_\infty & H^1(G_v,{\mathbb{Z}}/2{\mathbb{Z}}) & 0 & H^1_{nr}(G_v,{\mathbb{Z}}/2{\mathbb{Z}})=0 & H^1(G_v,\mu_2) \\ v\in Z_\infty \backslash X_\infty & H^1_{nr}(G_v,{\mathbb{Z}}/2{\mathbb{Z}})=0 & H^1(G_v,\mu_2) & H^1_{nr}(G_v,{\mathbb{Z}}/2{\mathbb{Z}})=0 & H^1(G_v,\mu_2) \\ v\in X_{<\infty} & H^1(G_v,{\mathbb{Z}}/p{\mathbb{Z}}) & 0 & H^1_{nr}(G_v,{\mathbb{Z}}/p{\mathbb{Z}}) & H^1_{nr}(G_v,\mu_p) \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l|cccc} & M_v & M^\perp_v & N_v & N^\perp_v \\ \hline\\[-9pt] v\in Z_p & H^1_{nr}(G_v,{\mathbb{Z}}/p{\mathbb{Z}}) & H^1_{f}(G_v,\mu_p) & H^1_{nr}(G_v,{\mathbb{Z}}/p{\mathbb{Z}}) & H^1_{f}(G_v,\mu_p) \\ v\in X_\infty & H^1(G_v,{\mathbb{Z}}/2{\mathbb{Z}}) & 0 & H^1_{nr}(G_v,{\mathbb{Z}}/2{\mathbb{Z}})=0 & H^1(G_v,\mu_2) \\ v\in Z_\infty \backslash X_\infty & H^1_{nr}(G_v,{\mathbb{Z}}/2{\mathbb{Z}})=0 & H^1(G_v,\mu_2) & H^1_{nr}(G_v,{\mathbb{Z}}/2{\mathbb{Z}})=0 & H^1(G_v,\mu_2) \\ v\in X_{<\infty} & H^1(G_v,{\mathbb{Z}}/p{\mathbb{Z}}) & 0 & H^1_{nr}(G_v,{\mathbb{Z}}/p{\mathbb{Z}}) & H^1_{nr}(G_v,\mu_p) \\ \end{array} \end{align*} $$
We now compute
![]() $ \dim M_v - \dim N_v$
. The first three entries of the table below are clear. As
$ \dim M_v - \dim N_v$
. The first three entries of the table below are clear. As
![]() $\delta (K_v)=1$
, local class field theory implies
$\delta (K_v)=1$
, local class field theory implies
![]() $\dim H^1(G_v, { {\mathbb Z}/p{\mathbb Z}}) =2$
. That
$\dim H^1(G_v, { {\mathbb Z}/p{\mathbb Z}}) =2$
. That
![]() $\dim H^1_{nr}(G_v, { {\mathbb Z}/p{\mathbb Z}}) =1$
follows as there is a unique unramified
$\dim H^1_{nr}(G_v, { {\mathbb Z}/p{\mathbb Z}}) =1$
follows as there is a unique unramified
![]() $ {\mathbb Z}/p{\mathbb Z} $
-extension of any local field. This establishes the last entry.
$ {\mathbb Z}/p{\mathbb Z} $
-extension of any local field. This establishes the last entry.
 $$ \begin{align*} \begin{array}{l|c} & \dim M_v - \dim N_v \\ \hline v\in Z_p & 0\\ v\in X_\infty & 1\\ v\in Z_\infty \backslash X_\infty & 0\\ v\in X_{<\infty} & 1\\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l|c} & \dim M_v - \dim N_v \\ \hline v\in Z_p & 0\\ v\in X_\infty & 1\\ v\in Z_\infty \backslash X_\infty & 0\\ v\in X_{<\infty} & 1\\ \end{array} \end{align*} $$
Applying the Greenberg–Wiles formula for
![]() $\{M_v\}_{v\in Z}$
and
$\{M_v\}_{v\in Z}$
and
![]() $\{N_v\}_{v\in Z}$
and subtracting the second equation from the first and recalling
$\{N_v\}_{v\in Z}$
and subtracting the second equation from the first and recalling
![]() $\#X=\#I + \# D =r+s$
:
$\#X=\#I + \# D =r+s$
:
 $$ \begin{align} \begin{array}{l} \dim H^1(G_X, { {\mathbb Z}/p{\mathbb Z}}) -\dim H^1(G_\emptyset, { {\mathbb Z}/p{\mathbb Z}})= \\ \dim H^1_{\mathcal M}(G_{Z}, { {\mathbb Z}/p{\mathbb Z}}) - \dim H^1_{\mathcal N}(G_{Z}, { {\mathbb Z}/p{\mathbb Z}}) =\\ \dim H^1_{{\mathcal M}^\perp}(G_{Z},\mu_p) - \dim H^1_{{\mathcal N}^\perp}(G_{Z},\mu_p) +\sum_{v\in Z} (\dim M_v - \dim N_v)=\\ \dim H^1_{{\mathcal M}^\perp}(G_{Z},\mu_p) - \dim H^1_{{\mathcal N}^\perp}(G_{Z},\mu_p) + r+s. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{l} \dim H^1(G_X, { {\mathbb Z}/p{\mathbb Z}}) -\dim H^1(G_\emptyset, { {\mathbb Z}/p{\mathbb Z}})= \\ \dim H^1_{\mathcal M}(G_{Z}, { {\mathbb Z}/p{\mathbb Z}}) - \dim H^1_{\mathcal N}(G_{Z}, { {\mathbb Z}/p{\mathbb Z}}) =\\ \dim H^1_{{\mathcal M}^\perp}(G_{Z},\mu_p) - \dim H^1_{{\mathcal N}^\perp}(G_{Z},\mu_p) +\sum_{v\in Z} (\dim M_v - \dim N_v)=\\ \dim H^1_{{\mathcal M}^\perp}(G_{Z},\mu_p) - \dim H^1_{{\mathcal N}^\perp}(G_{Z},\mu_p) + r+s. \end{array} \end{align} $$
To prove Proposition 2.2, we need to show this last quantity is
![]() $\dim R_X=s$
, the dimension of the space of dependence relations on the set
$\dim R_X=s$
, the dimension of the space of dependence relations on the set
![]() $\{\sigma _v\}_{v\in X} \subset W = \mathrm{Gal}(K'(\sqrt [p]{V_\emptyset })/K')$
.
$\{\sigma _v\}_{v\in X} \subset W = \mathrm{Gal}(K'(\sqrt [p]{V_\emptyset })/K')$
.
An element
![]() $f \in H^1_{{\mathcal N}^\perp }(G_{Z},\mu _p)$
gives rise to the field diagram below, where
$f \in H^1_{{\mathcal N}^\perp }(G_{Z},\mu _p)$
gives rise to the field diagram below, where
![]() $L_f/K'$
is a
$L_f/K'$
is a
![]() $ { {\mathbb Z}/p{\mathbb Z}}$
-extension peu ramifiée at
$ { {\mathbb Z}/p{\mathbb Z}}$
-extension peu ramifiée at
![]() $v\in Z_p$
, with no condition on
$v\in Z_p$
, with no condition on
![]() $v\in Z_\infty $
and unramified at
$v\in Z_\infty $
and unramified at
![]() $v\in X_{<\infty }$
. We show the composite of all such
$v\in X_{<\infty }$
. We show the composite of all such
![]() $L_f$
is
$L_f$
is
![]() $K'\left (\sqrt [p]{V_\emptyset }\right )$
.
$K'\left (\sqrt [p]{V_\emptyset }\right )$
.

By the nature of cohomology classes in
![]() $H^1(G_Z,\mu _p)$
, the extension
$H^1(G_Z,\mu _p)$
, the extension
![]() $L_f/K$
is Galois. Kummer Theory implies
$L_f/K$
is Galois. Kummer Theory implies
![]() $\alpha _f \in K'/{K'}^{\times p}$
, which decomposes into
$\alpha _f \in K'/{K'}^{\times p}$
, which decomposes into
![]() $\omega ^i$
-eigenspaces, where
$\omega ^i$
-eigenspaces, where
![]() $\omega :\mathrm{Gal}(K'/K) \to ( {\mathbb Z}/p{\mathbb Z} )^\times $
is the cyclotomic character given by
$\omega :\mathrm{Gal}(K'/K) \to ( {\mathbb Z}/p{\mathbb Z} )^\times $
is the cyclotomic character given by
![]() $\sigma (\zeta _p) =\zeta _p^{\omega (\sigma )}$
for
$\sigma (\zeta _p) =\zeta _p^{\omega (\sigma )}$
for
![]() $\zeta _p$
a primitive pth root of unity. As
$\zeta _p$
a primitive pth root of unity. As
![]() $\mu _p \simeq {\mathbb Z}/p{\mathbb Z} (\omega )$
, Kummer Theory gives the
$\mu _p \simeq {\mathbb Z}/p{\mathbb Z} (\omega )$
, Kummer Theory gives the
![]() $\mathrm{Gal}(K'/K)$
-equivariant pairing
$\mathrm{Gal}(K'/K)$
-equivariant pairing
That
![]() $f\in H^1(G_Z, {\mathbb Z}/p{\mathbb Z} (\omega ))$
implies
$f\in H^1(G_Z, {\mathbb Z}/p{\mathbb Z} (\omega ))$
implies
![]() $\mathrm{Gal}(L_f/K')$
is in the
$\mathrm{Gal}(L_f/K')$
is in the
![]() $\omega $
-eigenspace as is
$\omega $
-eigenspace as is
![]() $ {\mathbb Z}/p{\mathbb Z} (\omega )$
. Thus,
$ {\mathbb Z}/p{\mathbb Z} (\omega )$
. Thus,
![]() $\alpha _f $
is in the trivial eigenspace of
$\alpha _f $
is in the trivial eigenspace of
![]() $K^{\prime \times }/ K^{\prime \times p}$
. We will show we may assume
$K^{\prime \times }/ K^{\prime \times p}$
. We will show we may assume
![]() $\alpha _f \in K$
. If
$\alpha _f \in K$
. If
![]() $K'=K$
this is obvious so we assume
$K'=K$
this is obvious so we assume
![]() $1<d=[K':K] \mid p-1$
. Since
$1<d=[K':K] \mid p-1$
. Since
![]() $\alpha _f$
is in the trivial eigenspace,
$\alpha _f$
is in the trivial eigenspace,
![]() $N^{K'}_K(\alpha _f) \equiv \alpha ^d_f$
mod
$N^{K'}_K(\alpha _f) \equiv \alpha ^d_f$
mod
![]() $K^{\prime \times p}$
. But
$K^{\prime \times p}$
. But
![]() $N^{K'}_K(\alpha _f) \in K^\times $
and
$N^{K'}_K(\alpha _f) \in K^\times $
and
![]() $(d,p)=1$
so a suitable power
$(d,p)=1$
so a suitable power
![]() $N^{K'}_K(\alpha _f)^r$
is congruent to
$N^{K'}_K(\alpha _f)^r$
is congruent to
![]() $\alpha _f$
mod
$\alpha _f$
mod
![]() $K^{\prime \times p}$
. Just replace
$K^{\prime \times p}$
. Just replace
![]() $\alpha _f$
by
$\alpha _f$
by
![]() $N^{K'}_K(\alpha _f)^r \in K$
.
$N^{K'}_K(\alpha _f)^r \in K$
.
Since
![]() $L_f/K'$
is unramified at all finite tame v, we have
$L_f/K'$
is unramified at all finite tame v, we have
![]() $\alpha _f = u \pi _v^{pr}$
, where
$\alpha _f = u \pi _v^{pr}$
, where
![]() $u\in K_v$
is a unit and
$u\in K_v$
is a unit and
![]() $\pi _v$
is a uniformizer. At
$\pi _v$
is a uniformizer. At
![]() $v\in Z_p$
being peu ramifiée implies that locally at
$v\in Z_p$
being peu ramifiée implies that locally at
![]() $v\in X_p$
, we again have
$v\in X_p$
, we again have
![]() $\alpha _f = u \pi _v^{pr}$
. Together, these mean that the fractional ideal
$\alpha _f = u \pi _v^{pr}$
. Together, these mean that the fractional ideal
![]() $(\alpha _f)$
of K is a pth power, which implies that
$(\alpha _f)$
of K is a pth power, which implies that
![]() $\alpha _f \in V_\emptyset $
. Conversely, if
$\alpha _f \in V_\emptyset $
. Conversely, if
![]() $\alpha \in V_\emptyset $
, then, recalling that
$\alpha \in V_\emptyset $
, then, recalling that
![]() $(\alpha )=J^p$
for some ideal of K, we have that
$(\alpha )=J^p$
for some ideal of K, we have that
![]() $K'\left (\sqrt [p]{\alpha }\right )/K'$
is a
$K'\left (\sqrt [p]{\alpha }\right )/K'$
is a
![]() $ { {\mathbb Z}/p{\mathbb Z}}$
-extension peu ramifiée at
$ { {\mathbb Z}/p{\mathbb Z}}$
-extension peu ramifiée at
![]() $v\in Z_p$
, with no condition at
$v\in Z_p$
, with no condition at
![]() $v\in Z_\infty $
. Thus,
$v\in Z_\infty $
. Thus,
![]() $\alpha $
gives rise to an element
$\alpha $
gives rise to an element
![]() $f_\alpha \in H^1_{{\mathcal N}^\perp }(G_Z,\mu _p)$
so
$f_\alpha \in H^1_{{\mathcal N}^\perp }(G_Z,\mu _p)$
so
![]() $L:=K'\left ( \sqrt [p]{V_\emptyset }\right )$
is the composite of all
$L:=K'\left ( \sqrt [p]{V_\emptyset }\right )$
is the composite of all
![]() $L_f$
for
$L_f$
for
![]() $f \in H^1_{{\mathcal N}^\perp }(G_Z,\mu _p)$
and
$f \in H^1_{{\mathcal N}^\perp }(G_Z,\mu _p)$
and
![]() $\dim H^1_{{\mathcal N}^\perp }(G_Z,\mu _p)= \dim (V_\emptyset /K^{\times p})$
.
$\dim H^1_{{\mathcal N}^\perp }(G_Z,\mu _p)= \dim (V_\emptyset /K^{\times p})$
.
An element
![]() $f \in H^1_{{\mathcal M}^\perp }(G_{Z},\mu _p)$
gives rise to a
$f \in H^1_{{\mathcal M}^\perp }(G_{Z},\mu _p)$
gives rise to a
![]() $ { {\mathbb Z}/p{\mathbb Z}}$
-extension of
$ { {\mathbb Z}/p{\mathbb Z}}$
-extension of
![]() $K'$
peu ramifiée at
$K'$
peu ramifiée at
![]() $v\in Z_p$
and split completely at
$v\in Z_p$
and split completely at
![]() $v\in X$
. We denote the composite of all these fields by
$v\in X$
. We denote the composite of all these fields by
![]() $D \subset K'\left ( \sqrt [p]{V_\emptyset }\right )$
.
$D \subset K'\left ( \sqrt [p]{V_\emptyset }\right )$
.

Recall that r is the dimension of the space
![]() $\langle \sigma _v \rangle _{v\in X} \subset \mathrm{Gal}(L/K')$
. Clearly, D is the field fixed of
$\langle \sigma _v \rangle _{v\in X} \subset \mathrm{Gal}(L/K')$
. Clearly, D is the field fixed of
![]() $\langle \sigma _v\rangle _{v\in X}$
so
$\langle \sigma _v\rangle _{v\in X}$
so
![]() $\dim _{{\mathbb F}_p} \mathrm{Gal}\left ( K'\left ( \sqrt [p]{V_\emptyset }\right )/ D \right ) =r =\# I$
from the second section of this note. Thus,
$\dim _{{\mathbb F}_p} \mathrm{Gal}\left ( K'\left ( \sqrt [p]{V_\emptyset }\right )/ D \right ) =r =\# I$
from the second section of this note. Thus,
![]() $\dim H^1_{{\mathcal M}^\perp }(G_{Z},\mu _p)=\dim (V_\emptyset /K^{\times p}) -r $
so the right side of (3.1) is
$\dim H^1_{{\mathcal M}^\perp }(G_{Z},\mu _p)=\dim (V_\emptyset /K^{\times p}) -r $
so the right side of (3.1) is
proving Proposition 2.2.
Acknowledgment
We thank Brian Conrad for pointing out to us a proof of Lemma 3.1 and Peter Uttenthal for helpful suggestions. We are grateful to the referee for a careful reading of the manuscript and making many helpful suggestions.