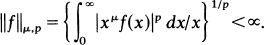Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1982.
Transmutation, Scattering Theory and Special Functions.
Vol. 69,
Issue. ,
p.
417.
Rooney, P. G.
1983.
On integral transformations with G-function kernels.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 93,
Issue. 3-4,
p.
265.
1985.
Transmutation Theory and Applications.
Vol. 117,
Issue. ,
p.
323.
Heywood, P.
and
Rooney, P.G.
1991.
On the inversion of the extended Hankel transformation.
Journal of Mathematical Analysis and Applications,
Vol. 160,
Issue. 1,
p.
284.
Heywood, P.
and
Rooney, P. G.
1994.
On the Struve Transformation.
SIAM Journal on Mathematical Analysis,
Vol. 25,
Issue. 2,
p.
450.
Rooney, P. G.
1995.
On the representation of functions by the Hankel and some related transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 125,
Issue. 3,
p.
449.
Tuan, Vu Kim
1997.
On the Range of the Hankel and Extended Hankel Transforms.
Journal of Mathematical Analysis and Applications,
Vol. 209,
Issue. 2,
p.
460.
Kilbas, A.A.
and
Borovco, A.N.
2000.
Hardy-Titchmarsh And Hankel Type Transforms In -Spaces.
Integral Transforms and Special Functions,
Vol. 10,
Issue. 3-4,
p.
239.
A.Kilbas, Anatoly
and
Trujillo, Juan J.
2000.
Generalized hankel transform no space.
Integral Transforms and Special Functions,
Vol. 9,
Issue. 4,
p.
271.
Airapetyan, Ruben
and
Witt, Ingo
2001.
Isometrim properties of the hankel transfromation in weighted sobolev spaces∗.
Integral Transforms and Special Functions,
Vol. 11,
Issue. 3,
p.
201.
Glaeske, Hans–Jürgen
and
Kilbas, Anatoly A.
2003.
A generalized Hankel transform on Lν,r–spaces.
Mathematische Nachrichten,
Vol. 258,
Issue. 1,
p.
16.
Al-Omari, Shrideh Khalaf
2019.
A study on a class of modified Bessel-type integrals in a Fréchet space of Boehmians.
Boletim da Sociedade Paranaense de Matemática,
Vol. 38,
Issue. 4,
p.
145.