No CrossRef data available.
Article contents
On the Closure of the Convex Hull of a Set
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let Y be a linear space over the complex plane C, and let F be a mapping on the complex linear space Y ⊕ C into subsets of C with the following properties: for y ∊ Y, λ and μ ∊ C, F(y + μ) is a nonempty and bounded subset of C, F(λy + μ) = λF(y) + μ and F(μ) = {μ}. We shall write f(y + μ) = sup{|λ + μ|: λ ∊ F(y)}, the radius of F(y + μ), y ∊ Y and μ ∊ C. The convex hull (resp. the closure) of a subset M of C is denoted by conv M (resp. 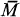 ).
).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1975
References
1.
Furata, T. and Nakamoto, R., On the numerical range of an operator, Proc. Japan Acad.
47 (1971), 279-284.Google Scholar
2.
Nieto, J. I., On Fredholm operators and the essential spectrum of singular integral operators, Math. Ann.
178 (1968), 62-77.Google Scholar
3.
Stampfli, J. G. and Williams, J. P., Growth conditions and the numerical range in a Banach algebra, Tôhoku Math. J.
20 (1968), 417-424.Google Scholar

