Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T13:59:48.876Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Coarse Geometry of James Spaces

Part of: Nonlinear functional analysis Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  16 December 2019

Gilles Lancien ,
Colin Petitjean  and
Antonin Procházka
Gilles Lancien
Affiliation:
Laboratoire de Mathématiques de Besançon, Université Bourgogne Franche-Comté, CNRS UMR-6623, 16 route de Gray, 25030 Besançon Cédex, Besançon, France Email: gilles.lancien@univ-fcomte.frantonin.prochazka@univ-fcomte.fr
Colin Petitjean
Affiliation:
Université Paris-Est Marne-la-Vallée, Laboratoire d’analyse et de mathématiques appliquées (UMR 8050), 5 boulevard Descartes, 77454 Marne-la-Vallée cedex 2, France Email: colin.petitjean@u-pem.fr
Antonin Procházka
Affiliation:
Laboratoire de Mathématiques de Besançon, Université Bourgogne Franche-Comté, CNRS UMR-6623, 16 route de Gray, 25030 Besançon Cédex, Besançon, France Email: gilles.lancien@univ-fcomte.frantonin.prochazka@univ-fcomte.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note we prove that the Kalton interlaced graphs do not equi-coarsely embed into the James space 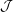${\mathcal{J}}$ nor into its dual 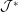${\mathcal{J}}^{\ast }$. It is a particular case of a more general result on the non-equi-coarse embeddability of the Kalton graphs into quasi-reflexive spaces with a special asymptotic structure. This allows us to exhibit a coarse invariant for Banach spaces, namely the non-equi-coarse embeddability of this family of graphs, which is very close to but different from the celebrated property 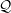${\mathcal{Q}}$ of Kalton. We conclude with a remark on the coarse geometry of the James tree space 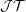${\mathcal{J}}{\mathcal{T}}$ and of its predual.

Keywords

non linear geometry of Banach spacecoarse embeddingJames space

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces
Secondary: 46B80: Nonlinear classification of Banach spaces; nonlinear quotients 46B85: Embeddings of discrete metric spaces into Banach spaces; applications in topology and computer science 46T99: None of the above, but in this section
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 1 , March 2020 , pp. 77 - 93
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first and third named authors are supported by the French “Investissements d’Avenir” program, project ISITE-BFC (contract ANR-15-IDEX-03).

References

Albiac, F. and Kalton, N. J., Topics in Banach Space Theory. Graduate Texts in Mathematics, 233, Springer, New York, 2006.Google Scholar
Argyros, S., Motakis, P., and Sari, B., A study of conditional spreading sequences. J. Funct. Anal. 273(2017), 3, 1205–1257. https://doi.org/10.1016/j.jfa.2017.04.009CrossRefGoogle Scholar
Baudier, F., Lancien, G., Motakis, P., and Schlumprecht, Th., A new coarsely rigid class of Banach spaces. 2018. arxiv:1806.00702.Google Scholar
Baudier, F., Lancien, G., and Schlumprecht, Th., The coarse geometry of Tsirelson’s space and applications. J. Amer. Math. Soc. 31(2018), 3, 699–717. https://doi.org/10.1090/jams/899CrossRefGoogle Scholar
Beauzamy, B. and Lapresté, J. T., Modèles étalés des espaces de Banach. Travaux en Cours, Hermann, Paris, 1984.Google Scholar
Bellenot, S. F., Haydon, R., and Odell, E., Quasi-reflexive and tree spaces constructed in the spirit of R. C. James. In: Contemp. Math.  Vol. 85. American Mathematical Society, Providence, RI, 1989, pp. 19–43. https://doi.org/10.1090/conm/085/983379Google Scholar
Causey, R. M. and Lancien, G., Prescribed Szlenk index of separable Banach spaces. Studia Math. 248(2019), 2, 109–127. https://doi.org/10.4064/sm171012-9-9CrossRefGoogle Scholar
Dilworth, S., Kutzarova, D., Lancien, G., and Randrianarivony, L., Equivalent norms with the property (𝛽) of Rolewicz. Rev. R. Acad. Cienc. Exactas, Fís. Nat. Ser. A Mat. RACSAM 111(2017), 1, 101–113. https://doi.org/10.1007/s13398-016-0278-2CrossRefGoogle Scholar
Freeman, D., Odell, E., Sari, B., and Zheng, B., On spreading sequences and asymptotic structures. Trans. Amer. Math. Soc. 370(2018), 6933–6953. https://doi.org/10.1090/tran/7189CrossRefGoogle Scholar
Gowers, W. T., Ramsey methods in Banach spaces. In: Handbook of the Geometry of Banach Spaces.  Vol. 2. North-Holland, Amsterdam, 2003, pp. 1071–1097. https://doi.org/10.1016/S1874-5849(03)80031-1CrossRefGoogle Scholar
James, R. C., Bases and reflexivity of Banach spaces. Ann. of Math. (2) 52(1950), 518–527. https://doi.org/10.2307/1969430CrossRefGoogle Scholar
James, R. C., A separable somewhat reflexive Banach space with nonseparable dual. Bull. Amer. Math. Soc. 80(1974), 738–743. https://doi.org/10.1090/S0002-9904-1974-13580-9CrossRefGoogle Scholar
Johnson, W. B., Lindenstrauss, J., Preiss, D., and Schechtman, G., Almost Fréchet differentiability of Lipschitz mappings between infinite-dimensional Banach spaces. Proc. London Math. Soc. (3) 84(2002), 3, 711–746. https://doi.org/10.1112/S0024611502013400CrossRefGoogle Scholar
Kalton, N. J., Coarse and uniform embeddings into reflexive spaces. Q. J. Math. 58(2007), 393–414. https://doi.org/10.1093/qmath/ham018CrossRefGoogle Scholar
Kalton, N. J., Uniform homeomorphisms of Banach spaces and asymptotic structure. Trans. Amer. Math. Soc. 365(2013), 1051–1079. https://doi.org/10.1090/S0002-9947-2012-05665-0CrossRefGoogle Scholar
Kalton, N. J. and Randrianarivony, L., The coarse Lipschitz geometry of ℓ p⊕ℓ q. Math. Ann. 341(2008), 1, 223–237. https://doi.org/10.1007/s00208-007-0190-3CrossRefGoogle Scholar
Lancien, G., Réflexivité et normes duales possèdant la propriété uniforme de Kadec-Klee. Publications Mathématiques de Besançon 14(1993/94).Google Scholar
Lancien, G. and Raja, M., Asymptotic and coarse Lipschitz structures of quasi-reflexive Banach spaces. Houston J. Math. 44(2018), 3, 927–940.Google Scholar
Milman, V. D., Geometric theory of Banach spaces. II. Geometry of the unit ball. (Russian). Uspehi Mat. Nauk 26(1971), 73–149.Google Scholar
Naor, A., L 1 embeddings of the Heisenberg group and fast estimation of graph isoperimetry. In: Proceedings of the International Congress of Mathematicians.  Vol. III. Hindustan Book Agency, New Delhi, 2010, pp. 1549–1575.Google Scholar
Nétillard, F., Coarse Lipschitz embeddings of James spaces. Bull. Belg. Math. Soc. Simon Stevin 25(2018), 71–84.Google Scholar
Schoenberg, I. J., Metric spaces and positive definite functions. Trans. Am. Math. Soc. 44(1938), 522–536. https://doi.org/10.2307/1989894CrossRefGoogle Scholar