Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pouzet, M.
1985.
Graphs and Order.
p.
592.
Morris, Joy
and
Šajna, Mateja
2005.
Brian Alspach and his work.
Discrete Mathematics,
Vol. 299,
Issue. 1-3,
p.
269.
Gao, Yinling
and
Yang, Yong
2022.
Bounding the orders of nilpotent subgroups of solvable linear groups.
Rocky Mountain Journal of Mathematics,
Vol. 52,
Issue. 5,

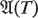 denote the automorphism group of the tournament
denote the automorphism group of the tournament  taken over all tournaments of order n. It was noted in [3] that
taken over all tournaments of order n. It was noted in [3] that 