Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Erdös, P.
and
Tenenbaum, G.
1989.
Sur les fonctions arithmétiques liées aux diviseurs consécutifs.
Journal of Number Theory,
Vol. 31,
Issue. 3,
p.
285.
Balog, Antal
Erdös, Paul
and
Tenenbaum, G.
1990.
Analytic Number Theory.
p.
77.
Sándor, J.
and
Crstici, B.
2004.
Handbook of Number Theory II.
p.
329.


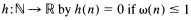 and
and 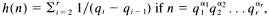 where
where 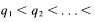
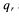 are primes and
are primes and 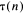 the number of divisors of
the number of divisors of 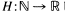 be defined by
be defined by 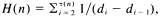 where
where 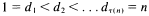 are the divisors of
are the divisors of 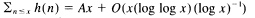 and
and