Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-15T08:32:35.588Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Distribution of Sum of Independent Positive Binomial Variables

Published online by Cambridge University Press:  20 November 2018

J. C. Ahuja
J. C. Ahuja*
Affiliation:
Portland State University, Portland, Oregon
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X1, X2, …, Xn be n independent and identically distributed random variables having the positive binomial probability function

1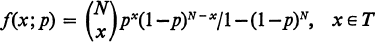

where 0 < p < 1, and T = {1, 2, …, N}. Define their sum as Y=X1 + X2 + … +Xn. The distribution of the random variable Y has been obtained by Malik [2] using the inversion formula for characteristic functions. It appears that his result needs some correction. The purpose of this note is to give an alternative derivation of the distribution of Y by applying one of the results, established by Patil [3], for the generalized power series distribution.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 1 , March 1970 , pp. 151 - 152
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Feller, W., An introduction to probability theory and its applications, Wiley, New York, 1 (third edition), 1968.Google Scholar
2. Malik, H. J., Distribution of the sum of truncated binomial variates. Canad. Math. Bull. 12 (1969), 334-336.Google Scholar
3. Patil, G. P., Minimum variance unbiased estimation and certain problems of additive number theory, Ann. Math. Statist. 34 (1963), 1050-1056.Google Scholar
4. Pearson, K., Tables of the incomplete beta function, Cambridge Univ. Press, London 1934.Google Scholar