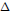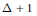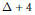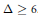Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Weifan
and
Zhang, Kemin
2005.
ENTIRE CHROMATIC NUMBER AND Δ-MATCHING OF OUTERPLANE GRAPHS.
Acta Mathematica Scientia,
Vol. 25,
Issue. 4,
p.
672.
Wu, Jian-liang
and
Wu, Yu-liang
2005.
The Entire Coloring of Series-Parallel Graphs.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 21,
Issue. 1,
p.
61.
Wang, Weifan
and
Lih, Ko‐Wei
2008.
Coupled choosability of plane graphs.
Journal of Graph Theory,
Vol. 58,
Issue. 1,
p.
27.
Hetherington, Timothy J.
2009.
Entire choosability of near-outerplane graphs.
Discrete Mathematics,
Vol. 309,
Issue. 8,
p.
2153.
Wang, Weifan
and
Zhu, Xuding
2011.
Entire colouring of plane graphs.
Journal of Combinatorial Theory, Series B,
Vol. 101,
Issue. 6,
p.
490.
Dong, Wei
2012.
A note on entire choosability of plane graphs.
Discrete Applied Mathematics,
Vol. 160,
Issue. 7-8,
p.
1257.
Wang, Yingqian
Mao, Xianghua
and
Miao, Zhengke
2013.
Plane Graphs with Maximum Degree Are Entirely ‐Colorable.
Journal of Graph Theory,
Vol. 73,
Issue. 3,
p.
305.
Borodin, O.V.
2013.
Colorings of plane graphs: A survey.
Discrete Mathematics,
Vol. 313,
Issue. 4,
p.
517.
Dong, Wei
and
Lin, Wensong
2014.
Entire coloring of plane graph with maximum degree eleven.
Discrete Mathematics,
Vol. 336,
Issue. ,
p.
46.
Wang, Yiqiao
Hu, Xiaoxue
and
Wang, Weifan
2014.
Planar Graphs with $\Delta\ge 9$ are Entirely $(\Delta+2)$-Colorable.
SIAM Journal on Discrete Mathematics,
Vol. 28,
Issue. 4,
p.
1892.
Wang, Yingqian
2014.
Entire(Δ+2)-colorability of plane graphs.
European Journal of Combinatorics,
Vol. 38,
Issue. ,
p.
110.
HU, XIAOXUE
and
WANG, YIQIAO
2014.
PLANE GRAPHS ARE ENTIRELY (Δ + 5)-CHOOSABLE.
Discrete Mathematics, Algorithms and Applications,
Vol. 06,
Issue. 02,
p.
1450023.
Hu, Xiaoxue
Wang, Weifan
Shiu, Wai Chee
and
Wang, Yiqiao
2016.
Plane graphs with maximum degree 9 are entirely 11-choosable.
Discrete Mathematics,
Vol. 339,
Issue. 11,
p.
2742.
Wang, Weifan
Wu, Tingting
Hu, Xiaoxue
and
Wang, Yiqiao
2016.
The entire choosability of plane graphs.
Journal of Combinatorial Optimization,
Vol. 31,
Issue. 3,
p.
1221.
Hu, Xiaoxue
Wang, Ping
Wang, Yiqiao
and
Wang, Weifan
2017.
The entire chromatic number of graphs embedded on the torus with large maximum degree.
Theoretical Computer Science,
Vol. 689,
Issue. ,
p.
108.
Hu, Xiaoxue
Wang, Weifan
Wang, Yiqiao
and
Wang, Ping
2018.
Entire Coloring of Graphs Embedded in a Surface of Nonnegative Characteristic.
Graphs and Combinatorics,
Vol. 34,
Issue. 6,
p.
1489.
Kong, Jiangxu
Hu, Xiaoxue
and
Wang, Yiqiao
2020.
Plane graphs with $$\Delta =7$$ are entirely 10-colorable.
Journal of Combinatorial Optimization,
Vol. 40,
Issue. 1,
p.
1.
Wang, Weifan
Hu, Xiaoxue
and
Wang, Yiqiao
2021.
Entire coloring of 2-connected plane graphs.
European Journal of Combinatorics,
Vol. 94,
Issue. ,
p.
103286.
Sun, Junwei
Xiao, Xiao
Liu, Peng
Wang, Yanfeng
and
Wang, Yingcong
2022.
Design and implementation of four-color conjecture circuit based on memristor neural network.
AEU - International Journal of Electronics and Communications,
Vol. 144,
Issue. ,
p.
154041.