Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T19:31:03.890Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Ergodic Hilbert Transform for Operators In Lp, 1 < p < ∞

Published online by Cambridge University Press:  20 November 2018

Ryotaro Sato
Ryotaro Sato*
Affiliation:
Department of Mathematics School of Science Okayama University Okayama, 700 Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper the ergodic Hilbert transform is investigated at the operator theoretic level. Let T be an invertible positive operator on Lp = Lp(X, , μ) for some fixed p, 1 < p < ∞, such that sup{||Tn||p: — ∞ < n < ∞} < ∞. It is proved that the limit

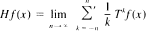
exists almost everywhere and in the strong operator topology, where the prime denotes that the term with zero denominator is omitted. Related results are also proved.

Keywords

47A35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 30 , Issue 2 , 01 June 1987 , pp. 210 - 214
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Akcoglu, M.A. and Kopp, P.E., Construction of dilations of positive Lp-contr actions, Math. Z. 155 (1977), pp. 119–127.Google Scholar
2. Akcoglu, M.A. and Sucheston, L., Dilations of positive contractions on Lp spaces, Canad. Math. Bull. 20(1977), pp. 285–292.Google Scholar
3. Calderón, A. P., Ergodic theory and translation-invariant operators, Proc. Nat. Acad. Sci. U.S.A. 59 (1968), pp. 349–353.Google Scholar
4. Campbell, J.T., Variations on the ergodic Hubert transform, Ph.D. thesis, University of North Carolina, Chapel Hill, 1984.Google Scholar
5. Campbell, J.T., Spectral analysis of the ergodic Hilbert transform, Indiana Univ. J. 35 (1986), 379–390.Google Scholar
6. Coifman, R.R. and Fefferman, C., Weighted norm inequalities for maximal functions and singular integrals, Studia Math. 51 (1974), pp. 241–250.Google Scholar
7. Cotlar, M., A unified theory of Hilbert transforms and ergodic theorems, Rev. Mat. Cuyana 1 (1955), pp. 105–167.Google Scholar
8. Dunford, N. and Schwartz, J.T., Linear Operators, Vol. I, Interscience, New York, 1958.Google Scholar
9. Hunt, R., Muckenhoupt, B. and Wheeden, R., Weighted norm inequalities for the conjugate function and Hilbert transform, Trans. Amer. Math. Soc. 176 (1973), pp. 227–251.Google Scholar
10. Ionescu-Tulcea, A., Ergodic properties of isometrics in Lp spaces, 1 < ρ < ∞, Bull. Amer. Math. Soc. 70 (1964), pp. 366–371.Google Scholar
11. Kan, C.H., Ergodic properties of Lamperti operators, Canad. J. Math. 30 (1978), pp. 1206–1214.Google Scholar
12. Petersen, K., Another proof of the existence of the ergodic Hilbert transform, Proc. Amer. Math. Soc. 88(1983), pp. 39–43.Google Scholar
13. Torre, A. de la, A simple proof of the maximal ergodic theorem, Canad. J. Math. 28 (1976), pp. 1073–1075.Google Scholar