Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T19:28:26.575Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Garsia Lie Idempotent

Published online by Cambridge University Press:  20 November 2018

Frédéric Patras ,
Christophe Reutenauer  and
Manfred Schocker
Frédéric Patras
Affiliation:
Laboratoire J.-A. Dieudonné, Université de Nice, Parc Valrose, 06108 Nice, cedex 02, France
Christophe Reutenauer
Affiliation:
Université du Québec á Montréal, Département de mathématiques, CP 8888, succ. Centre-Ville, Montréal, QC, H3C 3P8 e-mail: christo@math.uqam.ca
Manfred Schocker
Affiliation:
Department of Mathematics, University of Wales Swansea, Singleton Park, Swansea SA2 8PP, Wales, U.K.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The orthogonal projection of the free associative algebra onto the free Lie algebra is afforded by an idempotent in the rational group algebra of the symmetric group 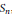${{S}_{n}}$, in each homogenous degree $n$. We give various characterizations of this Lie idempotent and show that it is uniquely determined by a certain unit in the group algebra of 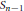${{S}_{n-1}}$. The inverse of this unit, or, equivalently, the Gram matrix of the orthogonal projection, is described explicitly. We also show that the Garsia Lie idempotent is not constant on descent classes (in fact, not even on coplactic classes) in 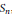${{S}_{n}}$.

Keywords

17B0105A9916S3017B60
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 3 , 01 September 2005 , pp. 445 - 454
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Bergeron, F., Bergeron, N., and Garsia, A. M., Idempotents for the free Lie algebra and q-enumeration. In: Invariant theory and tableaux, (Stanton, D., ed.) IMA Vol. Math. Appl. 19, Springer, New York, 1990, pp. 166–190.Google Scholar
[2] Blessenohl, D. and Laue, H., A basis construction for free Lie algebras. Exposition. Math. 11(1993), 145–152.Google Scholar
[3] Blessenohl, D. and Schocker, M., Noncommutative Character theory of symmetric Groups. Imperial College Press, London, 2005.Google Scholar
[4] Comtet, L., Sur les coefficients de l’inverse de la série formelle Σ n! tn . C.R. Acad. Sci. Paris Sér. A–B 275(1972), 569–572.Google Scholar
[5] Curtis, C.W. and Reiner, I., Representation theory of finite groups and associative algebras. John Wiley, New York, 1962.Google Scholar
[6] Duchamp, G., Orthogonal projection onto the free Lie algebra. Theor. Comput. Sci. 79(1991), 227–239.Google Scholar
[7] Garsia, A., Combinatorics of the free Lie algebra and the symmetric group. In: Analysis, et cetera. Academic Press, Boston, MA, 1990, pp. 309–382.Google Scholar
[8] Greene, C., An extension of Schensted's theorem. Adv. in Math. 14(1974), 254–265.Google Scholar
[9] Kljačko, A. A., Lie elements in the tensor algebra. Sibirsk. Mat. Ž. 15(1974), 914–920.Google Scholar
[10] Krob, D., Leclerc, B., and Thibon, J.-Y., Noncommutative symmetric functions. II. Transformations of alphabets. Internat. J. Algebra Comput. 7(1997), 181–264.Google Scholar
[11] Lothaire, M., Combinatorics on words. Addison Wesley, Reading, MA, 1983.Google Scholar
[12] Macdonald, I., Symmetric functions and Hall polynomials. Oxford Mathematical Monographs, The Clarendon Press, New York, 1979.Google Scholar
[13] Poirier, S. and Reutenauer, C., Algèbres de Hopf de tableaux. Ann. Sci. Math. Québec 19(1995), 79–90.Google Scholar
[14] Reutenauer, C., Free Lie algebras. LondonMathematical Society Monographs 7, Oxford University Press, New York, 1993.Google Scholar
[15] Sagan, B., The symmetric group, Wadsworth and Brooks/Cole, Pacific Grove, CA, 1991.Google Scholar
[16] Schocker, M., Lie elements and Knuth relations, Canad. J. Math. 56(2004), 871–882.Google Scholar
[17] Schocker, M., Über die höheren Lie-Darstellungen der symmetrischen Gruppen. Bayreuth. Math. Schr. 63(2001), 103–263.Google Scholar