Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T17:21:39.063Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Image of Certain Extension Maps. I

Published online by Cambridge University Press:  20 November 2018

Israel Moreno Mejía
Israel Moreno Mejía*
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autónoma de México, México, D.F. C.P. 04510, México e-mail: israel@matem.unam.mx
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 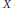$X$ be a smooth complex projective curve of genus 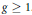$g\ge 1$. Let 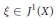$\xi \in {{J}^{1}}\left( X \right)$ be a line bundle on 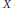$X$ of degree 1. Let 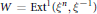$W=\text{Ex}{{\text{t}}^{1}}\left( {{\xi }^{n}},{{\xi }^{-1}} \right)$ be the space of extensions of 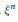${{\xi }^{n}}$ by 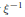${{\xi }^{-1}}$. There is a rational map 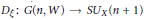${{D}_{\xi }}:G\left( n,W \right)\to S{{U}_{X}}\left( n+1 \right)$, where 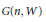$G\left( n,W \right)$ is the Grassmannian variety of $n$-linear subspaces of 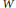$W$ and 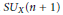$S{{U}_{X}}\left( n+1 \right)$ is the moduli space of rank 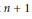$n+1$ semi-stable vector bundles on 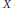$X$ with trivial determinant. We prove that if 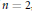$n=2$, then 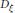${{D}_{\xi }}$ is everywhere defined and is injective.

Keywords

14H6014F0514D20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 3 , 01 September 2007 , pp. 427 - 433
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Atiyah, M. F.. Complex analytic connections in fibre bundles. Trans. Amer. Math. Soc. 85(1957), 181–207.Google Scholar
[2] Brambila-Paz, L., Grzegorczyk, I., and Newstead, P. E., Geography of Brill-Noether loci for small slopes. J. Algebraic Geom. 6(1997), no. 4, 645–669.Google Scholar
[3] Benson, D. J.. Representations and Cohomology. I. Second edition. Cambridge Studies in Advanced Mathematics 30, Cambridge University Press, Cambridge, 1998.Google Scholar
[4] Bertram, A., Moduli of rank-2 vector bundles, theta divisors, and the geometry of curves in projective space. J. Differential Geom. 35(1992), no. 2, 429–469.Google Scholar
[5] Lange, H. and Narasimhan, M. S.. Maximal subbundles of rank two vector bundles on curves. Math. Ann. 266(1983), no. 1, 55–72.Google Scholar
[6] Le Potier, J.. Lectures on Vector Bundles. Cambridge Studies in Advanced Mathematics 54, Cambridge University Press, Cambridge, 1997.Google Scholar
[7] Narasimhan, M. S. and Ramanan, S.. Moduli of vector bundles on a compact Riemann surface. Ann. of Math. 89(1969) 14–51.Google Scholar
[8] Narasimhan, M. S. and Seshadri, C. S., Stable and unitary vector bundles on a compact Riemann surface. Ann. of Math. 82(1965), 540–567.Google Scholar
[9] Seshadri, C. S., Space of unitary vector bundles on a compact Riemann surface. Ann. of Math. 85(1967), 303–336.Google Scholar