Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-24T04:02:38.939Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Maximum Order of the Group of a Tournament

Published online by Cambridge University Press:  20 November 2018

Myron Goldberg  and
J. W. Moon
Myron Goldberg
Affiliation:
University of Alberta, Edmonton
J. W. Moon
Affiliation:
University of Alberta, Edmonton
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A (round-robin) tournament Tn consists of n nodes p1, p2, …, Pn such that each pair of distinct nodes pi and pj is joined by one of the oriented arcs 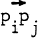or 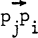. If the arc 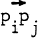is in Tn, then we say that pi. dominates pj. The set of all dominance-preserving permutations a of the nodes T form a group, the automorphism group G(T ) of Tn. It is known (see [1]) that there exist tournaments Tn whose group n G(Tn) is abstractly isomorphic to a given group H if and only if the order g(H) of H is odd.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 9 , Issue 5 , December 1966 , pp. 563 - 569
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Moon, J. W., Tournaments with a given automorphism group. Canad. J. Math., 16, (1964), pages 485-489.Google Scholar
2. Wielandt, H., Finite Permutation Groups. Trans, by Bercov, R., Academic Press, New York, (1964), page 5.Google Scholar