Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hanson, D.
1973.
On a Theorem of Sylvester and Schur.
Canadian Mathematical Bulletin,
Vol. 16,
Issue. 2,
p.
195.
Freitag, Artur
1977.
Einige Bemerkungen zur Verteilung der Gau�schen Primzahlen.
Archiv der Mathematik,
Vol. 29,
Issue. 1,
p.
93.
Kent, Clement F.
and
Hodgson, Bernard R.
1982.
An arithmetical characterization of NP.
Theoretical Computer Science,
Vol. 21,
Issue. 3,
p.
255.
Nicolas, J. L.
and
Robin, G.
1983.
Majorations Explicites Pour le Nombre de Diviseurs de N.
Canadian Mathematical Bulletin,
Vol. 26,
Issue. 4,
p.
485.
Babai, László
Goodman, Albert J.
and
Pyber, László
1993.
On faithful permutation representations of small degree.
Communications in Algebra,
Vol. 21,
Issue. 5,
p.
1587.
BALOG, ANTAL
PYBER, LÁSZLÓ
and
MANN, AVINOAM
2000.
POLYNOMIAL INDEX GROWTH GROUPS.
International Journal of Algebra and Computation,
Vol. 10,
Issue. 06,
p.
773.
Mann, A.
2001.
Groups generated by elements of small breadth.
Journal of Group Theory,
Vol. 4,
Issue. 3,
Feng, Bei-ye
2005.
An Simple Elementary Proof for the Inequality d n < 3 n.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 21,
Issue. 3,
p.
455.
Farhi, Bakir
2005.
Minorations non triviales du plus petit commun multiple de certaines suites finies d'entiers.
Comptes Rendus. Mathématique,
Vol. 341,
Issue. 8,
p.
469.
Hong, Shaofang
and
Feng, Weiduan
2006.
Lower bounds for the least common multiple of finite arithmetic progressions.
Comptes Rendus. Mathématique,
Vol. 343,
Issue. 11-12,
p.
695.
Farhi, Bakir
2007.
Nontrivial lower bounds for the least common multiple of some finite sequences of integers.
Journal of Number Theory,
Vol. 125,
Issue. 2,
p.
393.
Hong, Shaofang
and
Yang, Yujuan
2008.
On the periodicity of an arithmetical function.
Comptes Rendus. Mathématique,
Vol. 346,
Issue. 13-14,
p.
717.
Farhi, Bakir
and
Kane, Daniel
2008.
New results on the least common multiple of consecutive integers.
Proceedings of the American Mathematical Society,
Vol. 137,
Issue. 6,
p.
1933.
Hong, Shaofang
and
Kominers, Scott
2009.
Further improvements of lower bounds for the least common multiples of arithmetic progressions.
Proceedings of the American Mathematical Society,
Vol. 138,
Issue. 3,
p.
809.
Guo, Victor J. W.
2010.
On the Least Common Multiple of Q-Binomial Coefficients.
Integers,
Vol. 10,
Issue. 3,
Hong, Shaofang
and
Qian, Guoyou
2011.
The least common multiple of consecutive arithmetic progression terms.
Proceedings of the Edinburgh Mathematical Society,
Vol. 54,
Issue. 2,
p.
431.
Bordellès, Olivier
2012.
Arithmetic Tales.
p.
57.
QIAN, GUOYOU
TAN, QIANRONG
and
HONG, SHAOFANG
2012.
THE LEAST COMMON MULTIPLE OF CONSECUTIVE TERMS IN A QUADRATIC PROGRESSION.
Bulletin of the Australian Mathematical Society,
Vol. 86,
Issue. 3,
p.
389.
Hong, Shaofang
Qian, Guoyou
and
Tan, Qianrong
2012.
The least common multiple of a sequence of products of linear polynomials.
Acta Mathematica Hungarica,
Vol. 135,
Issue. 1-2,
p.
160.
Qian, Guoyou
and
Hong, Shaofang
2013.
Asymptotic behavior of the least common multiple of consecutive arithmetic progression terms.
Archiv der Mathematik,
Vol. 100,
Issue. 4,
p.
337.
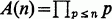 the above-mentioned product and define as usual
the above-mentioned product and define as usual