Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-14T09:10:52.019Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Property (PU) for *-Regular Rank Rings

Published online by Cambridge University Press:  20 November 2018

John L. Burke
John L. Burke*
Affiliation:
Department of Mathematics, University of Canterbury, Christchurch 1, New Zealand
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider an irreducible *-regular ring 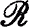with order k for some k≥4. If 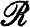is also a Baer ring it is a rank ring. Our first result is:

Theorem 1.3. Let 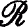be an irreducible *-regular Baer ring with order k for some k≥4. The following are equivalent.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 19 , Issue 1 , 01 March 1976 , pp. 21 - 38
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Halperin, Israel, Regular rank rings, Can. J. Math. 17 (1965), 709–719.Google Scholar
2. Halperin, Israel, Extension of the rank function, Studia Math. 27 (1966), 325–335.Google Scholar
3. Halperin, Israel, von Neumann’s manuscript on the inductive limit of regular rings. Can. J. Math. 20 (1968), 477–483.Google Scholar
4. Kaplansky, Irving, Any orthocomplemented complete modular lattice is a continuous geometry, Ann. of Math. 61 (1955), 524–541.Google Scholar
5. Kaplansky, Irving, Rings of operators (Benjamin, New York, 1968).Google Scholar
6. von Neumann, John, Continuous geometries with a transition probability, unpublished manuscript (reviewed by Israel Halperin in the Collected Works of John von Neumann, Pergamon, Elmsford, N.Y., 1962).Google Scholar
7. von Neumann, John, Continuous geometry (Princeton University Press, Princeton, 1960).Google Scholar
8. von Neumann, John, The non-isomorphism of certain continuous rings, Ann. of Math. 67 (1958), 485–496.Google Scholar
9. Prijatelj, N. and Vidav, I., On special *-regular rings, Michigan Math. J. 18 (1971), 213–221.Google Scholar
10. Vidav, I., On some *-regular rings, Acad. Serbe Sci. Publ. Inst. Math. 13 (1959), 73–80.Google Scholar