No CrossRef data available.
Article contents
On the Representation of Mappings of Tychonov Spaces as Restrictions of Linear Transformations
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let (X, τ) be a Tychonov space and 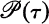 the collection of all families of pseudometrics on X generating the topology τ on X. Let f:X→X and c>0. Then f is said to be a topological c-homothety if there exists some B in
the collection of all families of pseudometrics on X generating the topology τ on X. Let f:X→X and c>0. Then f is said to be a topological c-homothety if there exists some B in 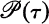 such that d(f(x), f(y))=cd(x, y) for all d ∈ B and all x, y in X (see [4]). We say that f can be linearized in L as a c-homothety if there exists a linear topological space L, and a topological embedding i:X→L such that i(f(x))=c i(x) for all x in X (see [4]).f is said to be squeezing if
such that d(f(x), f(y))=cd(x, y) for all d ∈ B and all x, y in X (see [4]). We say that f can be linearized in L as a c-homothety if there exists a linear topological space L, and a topological embedding i:X→L such that i(f(x))=c i(x) for all x in X (see [4]).f is said to be squeezing if 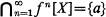 for some a in X.
for some a in X.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1976
References
1.
Edelstein, M., On the representation of mappings of compact metrizable spaces as restrictions of linear transformations, Can. J. Math. Vol. XXII (1970) 372–375.Google Scholar
2.
Edelstein, M. and Swaminathan, S., On the representation of mappings of normal Hausdorff spaces as restrictions of linear transformations, Roma Accademia Nazionale Del Lindel. Serie VIII, Vol. L (1971) 676–678.Google Scholar
3.
Gillman, L. and Jerison, M., Rings of continuous functions, Van Nostrand, Princeton, N.J. (1960).Google Scholar
4.
Janos, L., Topological homothetics on compact Hausdorff spaces, Proc. Amer. Math. Soc. Vol.
21 (1969) 562–568.Google Scholar

