Article contents
On the Set of Common Differences in van der Waerden’s Theorem on Arithmetic Progressions
Published online by Cambridge University Press: 20 November 2018
Abstract
Analogues of van der Waerden’s theorem on arithmetic progressions are considered where the family of all arithmetic progressions, 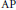 $\text{AP}$ , is replaced by some subfamily of
$\text{AP}$ , is replaced by some subfamily of 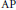 $\text{AP}$ . Specifically, we want to know for which sets
$\text{AP}$ . Specifically, we want to know for which sets 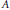 $A$ , of positive integers, the following statement holds: for all positive integers
$A$ , of positive integers, the following statement holds: for all positive integers  $r$ and
$r$ and 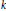 $k$ , there exists a positive integer
$k$ , there exists a positive integer 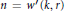 $n={w}'\text{(}k,r)$ such that for every
$n={w}'\text{(}k,r)$ such that for every  $r$ -coloring of
$r$ -coloring of 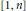 $[1,\,n]$ there exists a monochromatic
$[1,\,n]$ there exists a monochromatic 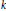 $k$ -term arithmetic progression whose common difference belongs to
$k$ -term arithmetic progression whose common difference belongs to 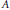 $A$ . We will call any subset of the positive integers that has the above property large. A set having this property for a specific fixed
$A$ . We will call any subset of the positive integers that has the above property large. A set having this property for a specific fixed  $r$ will be called
$r$ will be called  $r$ -large. We give some necessary conditions for a set to be large, including the fact that every large set must contain an infinite number of multiples of each positive integer. Also, no large set
$r$ -large. We give some necessary conditions for a set to be large, including the fact that every large set must contain an infinite number of multiples of each positive integer. Also, no large set 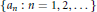 $\{{{a}_{n}}\,:\,n\,=\,1,\,2,\ldots \}$ can have
$\{{{a}_{n}}\,:\,n\,=\,1,\,2,\ldots \}$ can have  $\underset{n\to \infty }{\mathop{\lim \,\inf }}\,\,\frac{{{a}_{n+1}}}{{{a}_{n}}}\,>\,1$ . Sufficient conditions for a set to be large are also given. We show that any set containing
$\underset{n\to \infty }{\mathop{\lim \,\inf }}\,\,\frac{{{a}_{n+1}}}{{{a}_{n}}}\,>\,1$ . Sufficient conditions for a set to be large are also given. We show that any set containing  $n$ -cubes for arbitrarily large
$n$ -cubes for arbitrarily large  $n$ , is a large set. Results involving the connection between the notions of “large” and “2-large” are given. Several open questions and a conjecture are presented.
$n$ , is a large set. Results involving the connection between the notions of “large” and “2-large” are given. Several open questions and a conjecture are presented.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1999
References
- 18
- Cited by

