Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T06:01:56.085Z Has data issue: false hasContentIssue false
  • English
  • Français

On Two Functional Equations for the Trigonometric Functions

Published online by Cambridge University Press:  20 November 2018

Hiroshi Haruki
Hiroshi Haruki*
Affiliation:
University of Waterloo, Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the following cosine and sine functional equations:

(1)

(2)

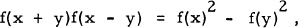
where f is an entire function of a complex variable z and x, y are complex variables [1; 2; 3].

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 12 , Issue 3 , June 1969 , pp. 281 - 286
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Aczel, J., Lectures on functional equations and their applications. (Academic Press, New York-London 1966) 117–128, 136–139.Google Scholar
2. Vincze, E., A d'alembert-Poisson fuggvenyegyenlet egyik altalanositasa. Mat. Lapok 12 (1961) 18–31.Google Scholar
3. Wilson, W. H., On certain related functional equations. Bull. Amer. Math. Soc. 26 (1919) 300–312.Google Scholar
4. Polya, G. and Szegö, G., Aufgaben und Eehrsatze ans der Analysis I. (Springer-Verlag, Berlin-Gottingen-Heidelberg 1954) 94.Google Scholar