Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T05:45:58.020Z Has data issue: false hasContentIssue false
  • English
  • Français

On Ulam Stability of a Functional Equation in Banach Modules

Published online by Cambridge University Press:  20 November 2018

Lahbib Oubbi
Lahbib Oubbi*
Affiliation:
Department ofMathematics, École Normale Supérieure, Mohammed V University of Rabat, PO Box 5118, Takaddoum, 10105 Rabat (Morocco) e-mail: oubbi@daad-alumni.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $X$ and $Y$ be Banach spaces and let 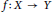$f\,:\,X\,\to \,Y$ be an odd mapping. For any rational number 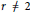$r\,\ne \,2$, C. Baak, D. H. Boo, and Th. M. Rassias proved the Hyers–Ulam stability of the functional equation

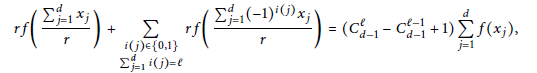$$rf\left( \frac{\sum\nolimits_{j=1}^{d}{{{x}_{j}}}}{r} \right)\,+\,\sum\limits_{\begin{smallmatrix} i\left( j \right)\,\in \left\{ 0,\,1 \right\} \\ \sum\nolimits_{j=1}^{d}{i\left( j \right)=\ell } \end{smallmatrix}}{rf\left( \frac{\sum\nolimits_{j=1}^{d}{{{\left( -1 \right)}^{i\left( j \right)}}{{x}_{j}}}}{r} \right)}\,=\,\left( C_{d-1}^{\ell }\,-\,C_{d-1}^{\ell -1}\,+\,1 \right)\,\sum\limits_{j=1}^{d}{f\left( {{x}_{j}} \right),}$$

where $d$ and $\ell$ are positive integers so that 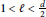$1\,<\,\ell \,<\,\frac{d}{2}$, and 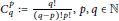$C_{q}^{p}\,:=\frac{q!}{\left( q-p \right)!p!},\,p,\,q\,\in \,\mathbb{N}$ with 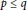$p\,\le \,q$.

In this note we solve this equation for arbitrary nonzero scalar $r$ and show that it is actually Hyers–Ulam stable. We thus extend and generalize Baak et al.’s result. Other questions concerning the $^{*}$-homomorphisms and the multipliers between 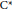${{C}^{*}}$-algebras are also considered.

Keywords

39A3039B1039A0646Hxxlinear functional equationHyers-Ulam stabilityBanach modulesC*-algebra homomorphisms
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 1 , 01 March 2017 , pp. 173 - 183
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Abdollahpoura, M. R., Aghayaria, R., and Rassias, Th. M., Hyers-Ulam stability of associated Laguerre differential equations in a subclass of analytic functions. J. Math. Anal. Appl. 437(2016), 605–612. http://dx.doi.Org/10.101 6/j.jmaa.2O1 6.01.024 Google Scholar
[2] Baak, C., Boo, D. H., and Rassias, Th. M., Generalized additive mapping in Banach modules and isomorphisms between C* -algebras. J. Math. Anal. Appl. 314(2006), 150–161. http://dx.doi.Org/10.1016/j.jmaa.2005.03.099 Google Scholar
[3] Blackadar, B., Operator algebras. Theory of C* -algebras and von Neumann algebras. Encyclopedia of Mathematical Sciences, 122, Springer-Verlag, Berlin, 2006. http://dx.doi.Org/10.1007/3-540-28517-2 Google Scholar
[4] Brzdek, J., On a method of proving the Hyers-Ulam stability of functional equations on restricted domains. Aust. J. Math. Anal. Appl. 6(2009), no. 1, Art. 4.Google Scholar
[5] Càdariu, L. and Radu, V., Fixed points and the stability of the Jensen's functional equation. J. Inequal. Pure Appl. Math. 4(2003), no. 1, Art. 4.Google Scholar
[6] Càdariu, L. and Radu, V., On the stability of the Cauchy functional equation: a fixed point approach. In: Interation Theory (ECIT ‘02), Grazer Math. Ber., 346, Karl-Franzens-Univ. Graz, Graz, 2004, pp. 43–52.Google Scholar
[7] Eshaghi, M. Gordji, Karimi, T., and S. Kaboli Gharetapeh, Approximately n-Jordan homomorphisms on Banach algebras. J. Inequal. Appl., 2009, Art. ID 870843. http://dx.doi.Org/10.1155/2009/870843 Google Scholar
[8] Forti, G.-L., Comments on the core of the direct method for proving Hyers-Ulam stability of functional equations. J. Math. Anal. Appl. 295(2004), no. 1,127-133. http://dx.doi.Org/10.1016/j.jmaa.2 004.03.011 Google Scholar
[9] Gàvruta, P., A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. J. Math. Anal. Appl. 184(1994), no. 3, 431–436. http://dx.doi.Org/10.1006/jmaa.1994.1211 Google Scholar
[10] Hyers, D. H., On the stability of the linear functional equation. Proc. Nat. Acad. Sci. U.S.A. 27(1941), 222–224. http://dx.doi.Org/10.1073/pnas.27.4.222 Google Scholar
[11] Jun, K.-W. and Kim, H. M., Remarks on the stability of additive functional equation. Bull. Korean Math. Soc. 38(2001), no. 4, 679–687.Google Scholar
[12] Jung, S.-M., Hyers-Ulam-Rassias stability of functional equations in nonlinear analysis. Springer Optimization and Its Applications, 48, Springer, New York, 2011. http://dx.doi.Org/10.1007/978-1-4419-9637-4 Google Scholar
[13] Jung, S.-M., Popa, D., and Rassias, Th. M., On the stability of the linear functional equation in a single variable on complete metric groups. J. Global Optim. 59(2014), 165–171. http://dx.doi.Org/10.1007/s10898-013-0083-9 Google Scholar
[14] Kannappan, PI., Functional equations and inequations with applications. Springer, New York, 2009. http://dx.doi.Org/10.1007/978-0-387-89492-8 Google Scholar
[15] Lee, J. R. and D. Y Shin, On the Cauchy-Rassias stability of a generalized additive functional equation. J. Math. Anal. Appl. 339(2008), 372–383. http://dx.doi.Org/10.1016/j.jmaa.2007.06.060.Google Scholar
[16] Mortici, C., Rassias, Th. M., and S. -M. Jung, On the stability of a functional equation associated with the Fibonacci numbers. Abs. Appl. Anal., 2014, Art. ID 546046. http://dx.doi.Org/10.11 55/2014/546046 Google Scholar
[17] Oubbi, L., Ulam-Hyers-Rassias stability problem for several kinds of mappings. Afr. Mat. 24(2013), no. 4, 525–542. http://dx.doi.Org/10.1007/s13370-012-0078-6 Google Scholar
[18] Oubbi, L., Stability of mappings from a ring A into an A-bimodule. Commun. Korean Math. Soc. 28(2013), no. 4, 767–782. http://dx.doi.Org/10.4134/CKMS.2013.28.4.767 Google Scholar
[19] Park, C., Automorphisms on a C* -algebra and isomorphisms between Lie JC* -algebras associated with a generalized additive mapping. Houston J. Math. 33(2007), no. 3, 815–837.Google Scholar
[20] Park, C. and Rassias, J. M., Stability of the Jensen-type functional equation in C* -algebras: a fixed point approach. Abstr. Appl. Anal., 2009, Art. ID 360432. http://dx.doi.Org/10.1155/2009/360432 Google Scholar
[21] Park, C. and Rassias, J. M., Fixed point and stability of the Cauchy functional equation. Aust. J. Math. Anal. Appl. 6(2009), no. 1, Art. 14.Google Scholar
[22] Park, C. and Saadati, R., Approximation of a generalized additive mapping in multi-Banach modules and isomorphisms in multi-C* -algebras: a fixed point approach. Adv. Difference Equ., 2012:162.Google Scholar
[23] Rassias, Th. M., On the stability of the linear mapping in Banach spaces. Proc. Amer. Math. Soc. 72(1978), 297–300. http://dx.doi.Org/10.1090/S0002-9939-1978-0507327-1 Google Scholar
[24] Sahoo, P. K. and Kannappan, P., Introduction to functional equations. CRC Press, Boca Raton, FL, 2011.Google Scholar
[25] Ulam, S. M., Problems in modern mathematics. Science Editions, Wiley, New York, 1964.Google Scholar