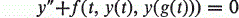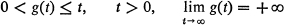Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Allegretto, W.
1974.
Oscillation Criteria for Quasilinear Equations.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 4,
p.
931.
Chiou, Kuo-liang
1974.
Oscillation and nonoscillation theorems for second order functional differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 45,
Issue. 2,
p.
382.
Nababan, S.
and
Noussair, E.S.
1976.
Oscillation criteria for second order nonlinear delay inequalities.
Bulletin of the Australian Mathematical Society,
Vol. 14,
Issue. 3,
p.
331.
Liu, Tsai-Sheng
1976.
Classification of solutions of higher-order differential equations and inequalities with deviating arguments.
Journal of Differential Equations,
Vol. 21,
Issue. 2,
p.
417.
Erbe, L.
1976.
Oscillation and Asymptotic Behavior of Solutions of Third order Differential Delay Equations.
SIAM Journal on Mathematical Analysis,
Vol. 7,
Issue. 4,
p.
491.
Nababan, S.
1978.
Oscillation criteria for a class of nonlinear vector delay-differential equations.
Annali di Matematica Pura ed Applicata,
Vol. 117,
Issue. 1,
p.
55.
Sficas, Y.G.
1979.
On the behavior of nonoscillatory solutions of differential equations with deviating argument.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 3,
Issue. 3,
p.
379.
Yan, Jurang
1987.
Oscillatory property for second order linear delay differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 122,
Issue. 2,
p.
380.
Grace, S.R
and
Lalli, B.S
1987.
An oscillation criterion for certain second order strongly sublinear differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 123,
Issue. 2,
p.
584.
Werbowski, Jaroslaw
1987.
Oscillations of differential inequalities caused by several delay arguments.
Journal of Mathematical Analysis and Applications,
Vol. 124,
Issue. 1,
p.
200.
Hamedani, G.G
1988.
Oscillation theorems for second order functional differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 135,
Issue. 1,
p.
237.
Erbe, L.H.
and
Zhang, B.G.
1989.
Oscillation of second order neutral differential equations.
Bulletin of the Australian Mathematical Society,
Vol. 39,
Issue. 1,
p.
71.
Hamedani, G.G.
and
Krenz, Gary S.
1989.
Oscillation theorems for nth-order functional differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 141,
Issue. 2,
p.
389.
Hamedani, G.G.
and
Krenz, Gary S.
1990.
Oscillation criteria for certain second order differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 149,
Issue. 1,
p.
271.
Thavaneswaran, A.
Samanta, M.
and
Qrdoukhani, N.
1991.
A note on recursive smoothers for semimartingales.
Communications in Statistics - Theory and Methods,
Vol. 20,
Issue. 7,
p.
2281.
Džurina, Jozef
and
Šoltés, Vincent
1996.
Asymptotic analysis of ODEs.
Journal of Computational and Applied Mathematics,
Vol. 67,
Issue. 2,
p.
301.
Agarwal, R.P.
Shieh, Shiow-Ling
and
Yeh, Cheh-Chih
1997.
Oscillation criteria for second-order retarded differential equations.
Mathematical and Computer Modelling,
Vol. 26,
Issue. 4,
p.
1.
Wang, Jingfa
1997.
Oscillation and nonoscillation theorems for a class of second order quasilinear functional-differential equations.
Hiroshima Mathematical Journal,
Vol. 27,
Issue. 3,
Huei-Lin, Hong
Fu-Hsiang, Wong
and
Cheh-Chih, Yeh
1999.
Classification of positive solutions of generalized functional differential equations.
Mathematical and Computer Modelling,
Vol. 30,
Issue. 5-6,
p.
89.
Rogovchenko, Yuri V
1999.
Oscillation Criteria for Certain Nonlinear Differential Equations.
Journal of Mathematical Analysis and Applications,
Vol. 229,
Issue. 2,
p.
399.