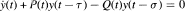Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yu, Jianshe
and
Wang, Zhicheng
1992.
Some further results on oscillation of neutral differential equations.
Bulletin of the Australian Mathematical Society,
Vol. 46,
Issue. 1,
p.
149.
Georgiou, D. A.
and
Qian, C.
1992.
Oscillation of Systems of Neutral Equations with Variable Coefficients.
Mathematische Nachrichten,
Vol. 155,
Issue. 1,
p.
99.
Grace, S.R.
1994.
Oscillation of certain functional differential equations.
Computers & Mathematics with Applications,
Vol. 27,
Issue. 4,
p.
91.
Oláh, Rudolf
1995.
Oscillation of differential equation of neutral type.
Hiroshima Mathematical Journal,
Vol. 25,
Issue. 1,
Li, Bingtuan
1996.
Oscillation of first order delay differential equations.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 12,
p.
3729.
Youshan, Tao
and
Guozhu, Gao
1998.
Oscillation of forced neutral differential equations with positive and negative coefficients.
Applied Mathematics-A Journal of Chinese Universities,
Vol. 13,
Issue. 3,
p.
271.
Tang, Xianhua
and
Shen, Jianhua
1998.
Oscillations of Delay Differential Equations with Variable Coefficients.
Journal of Mathematical Analysis and Applications,
Vol. 217,
Issue. 1,
p.
32.
Zhang, Xiaosheng
and
Yan, Jurang
2001.
Oscillation Criteria for First Order Neutral Differential Equations with Positive and Negative Coefficients.
Journal of Mathematical Analysis and Applications,
Vol. 253,
Issue. 1,
p.
204.
Shen, J.H.
and
Debnath, L.
2001.
Oscillations of solutions of neutral differential equations with positive and negative coefficients.
Applied Mathematics Letters,
Vol. 14,
Issue. 6,
p.
775.
Berezansky, Leonid
Domshlak, Yury
and
Braverman, Elena
2002.
On oscillation properties of delay differential equations with positive and negative coefficients.
Journal of Mathematical Analysis and Applications,
Vol. 274,
Issue. 1,
p.
81.
Luo, Zhiguo
and
Shen, Jianhua
2004.
Oscillation and Nonoscillation of Neutral Differential Equations with Positive and Negative Coefficients.
Czechoslovak Mathematical Journal,
Vol. 54,
Issue. 1,
p.
79.
2004.
Nonoscillation and Oscillation Theory for Functional Differential Equations.
p.
359.
Manojlović, J.
Shoukaku, Y.
Tanigawa, T.
and
Yoshida, N.
2006.
Oscillation criteria for second order differential equations with positive and negative coefficients.
Applied Mathematics and Computation,
Vol. 181,
Issue. 2,
p.
853.
Öcalan, Özkan
2007.
Oscillation of neutral differential equation with positive and negative coefficients.
Journal of Mathematical Analysis and Applications,
Vol. 331,
Issue. 1,
p.
644.
Öcalan, Özkan
2007.
Oscillation of forced neutral differential equations with positive and negative coefficients.
Computers & Mathematics with Applications,
Vol. 54,
Issue. 11-12,
p.
1411.
Shen, Jianhua
and
Zou, Ziran
2008.
Oscillation criteria for first-order impulsive differential equations with positive and negative coefficients.
Journal of Computational and Applied Mathematics,
Vol. 217,
Issue. 1,
p.
28.
Öcalan, Özkan
2009.
Existence of positive solutions for a neutral differential equation with positive and negative coefficients.
Applied Mathematics Letters,
Vol. 22,
Issue. 1,
p.
84.
Karpuz, Başak
and
Öcalan, Özkan
2009.
Necessary and sufficient conditions on asymptotic behaviour of solutions of forced neutral delay dynamic equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 7-8,
p.
3063.
Liu, Zeqing
Kang, Shin Min
and
Ume, Jeong Sheok
2010.
Existence of bounded nonoscillatory solutions of first-order nonlinear neutral delay differential equations.
Computers & Mathematics with Applications,
Vol. 59,
Issue. 11,
p.
3535.
Agarwal, Ravi P.
Berezansky, Leonid
Braverman, Elena
and
Domoshnitsky, Alexander
2012.
Nonoscillation Theory of Functional Differential Equations with Applications.
p.
59.