Published online by Cambridge University Press: 20 November 2018
Recently, Ronveaux [11] has shown how to use a combination of a Riccati transformation and a homographie transformation to estimate both from below and above the distance between a zero and the succeeding or preceding extremum (zero of y' ) of solutions of
1.1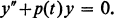
In this paper, we show how such transformations can be used to derive an equation from which the distance between successive zeros of a solution y of (1.1) can be estimated directly.
Research supported, in part, by National Research Council of Canada Grant A3053 to the Univ. of Alberta.