Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T16:22:44.585Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillation Theorems for Nonlinear Ordinary Differential Equations of Even Order

Published online by Cambridge University Press:  20 November 2018

Kurt Kreith  and
Takaŝi Kusano
Kurt Kreith
Affiliation:
University of California, DavisHiroshima University
Takaŝi Kusano
Affiliation:
University of California, DavisHiroshima University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the differential equation

1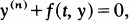

where n is even and f(t, y) is subject to the following conditions:

(a) f(t, y) is continuous on [0, ∞)× R;

(2) (b) f(t, y) is nondecreasing in y for each fixed t∈[0,∞);

(c) yf(t, y ) > 0 for y ≠ 0 and t∈[0,∞).

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 24 , Issue 4 , 01 December 1981 , pp. 409 - 413
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Atkinson, F. V., On second-order non-linear oscillations, Pacific J. Math. 5 (1955), 643-647.Google Scholar
2. Belohorec, Š., Oscilatorické riešenia istej nelinéarnej deferencíalnej rownice druhého rádu, Math. -Fyz. Časopis Sloven. Akad. Ved. 11 (1961), 250-255.Google Scholar
3. Burton, T. A., Non-continuation of solutions of differential equations of order N, Atti. Accad. Naz. Lincei Rend. LIX (1975), 706-711.Google Scholar
4. Coffman, C. V. and Wong, J. S. W., On a second order nonlinear oscillation problem, Trans. Amer. Math. Soc. 147 (1970), 357-366.Google Scholar
5. Coffman, C. V. and Wong, J. S. W., Oscillation and nonoscillation of solutions of generalized Emden-Fowler equations, Trans. Amer. Math. Soc. 167 (1972), 399-434.Google Scholar
6. Izjumova, D. V., On the conditions of oscillation and non-oscillation of second order nonlinear differential equations, Differencial'nye Uravnenij. 2 (1966), 1572-1585. (Russian)Google Scholar
7. Kiguradze, I. T., On oscillation of solutions of some ordinary differential equations, Dokl. Akad. Nauk SSS. 144 (1962), 33-36. (Russian)Google Scholar
8. Kiguradze, I. T., On the oscillation of solutions of the equation dmu/dtm + a(t) |u|n sign u =0, Mat. Sb. 65 (1964), 172-187. (Russian)Google Scholar
9. Kiguradze, I. T., The problem of oscillation of solutions of nonlinear differential equations, Differencial'nye Uravnenij. 1 (1965), 995-1006. (Russian)Google Scholar
10. Kiguradze, I. T., Some Singular Boundary Value Problems for Ordinary Differential Equations, Tbilsi University Press (1975), Tbilsi.Google Scholar
11. Kusano, T. and Onose, H., Oscillation of solutions of nonlinear differential delay equations of arbitrary order, Hiroshima Math. J. 2 (1972), 1-13.Google Scholar
12. Ličko, I. and Švec, M., Le caractère oscillatoire des solutions de l'équation y(n)+f(x)yα =0, n > l, Czechoslovak Math. J. 13 (1963), 481-491.+l,+Czechoslovak+Math.+J.+13+(1963),+481-491.>Google Scholar
13. Macki, J. W. and Wong, J. S. W., Oscillation of solutions of second order nonlinear differential equations, Pacific J. Math. 24 (1968), 111-118.Google Scholar
14. Onose, H., Oscillation and asymptotic behavior of solutions of retarded differential equations of arbitrary order, Hiroshima Math. J. 3 (1973), 333-360.Google Scholar
15. Ryder, G. H. and Wend, D. V. V., Oscillation of solutions of certain ordinary differential equations of n-th order, Proc. Amer. Math. Soc. 25 (1970), 463-469.Google Scholar