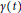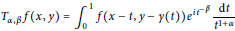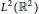Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Jiecheng
Fan, Dashan
and
Wang, Meng
2019.
Oscillatory hyper Hilbert transforms along variable curves.
Frontiers of Mathematics in China,
Vol. 14,
Issue. 4,
p.
673.