No CrossRef data available.
Published online by Cambridge University Press: 26 January 2023
Let G be a simple algebraic group of adjoint type over an algebraically closed field k of bad characteristic. We show that its sheets of conjugacy classes are parametrized by G-conjugacy classes of pairs 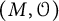 $(M,{\mathcal O})$ where M is the identity component of the centralizer of a semisimple element in G and
$(M,{\mathcal O})$ where M is the identity component of the centralizer of a semisimple element in G and 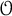 ${\mathcal O}$ is a rigid unipotent conjugacy class in M, in analogy with the good characteristic case.
${\mathcal O}$ is a rigid unipotent conjugacy class in M, in analogy with the good characteristic case.
The authors acknowledge support by: DOR2207212/22 “Algebre di Nichols, algebre di Hopf e gruppi algebrici” and BIRD203834 “Grassmannians, flag varieties and their generalizations” funded by the University of Padova. They are members of the INdAM group GNSAGA.