Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T21:05:51.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Percolation on Penrose Tilings

Published online by Cambridge University Press:  20 November 2018

A. Hof
A. Hof*
Affiliation:
Department of Mathematics and Statistics McMaster University Hamilton, Ontario L8S 4K1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In Bernoulli site percolation on Penrose tilings there are two natural definitions of the critical probability. This paper shows that they are equal on almost all Penrose tilings. It also shows that for almost all Penrose tilings the number of infinite clusters is almost surely 0 or 1. The results generalize to percolation on a large class of aperiodic tilings in arbitrary dimension, to percolation on ergodic subgraphs of 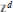${{\mathbb{Z}}^{d}}$, and to other percolation processes, including Bernoulli bond percolation.

Keywords

60K3582B43
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 2 , 01 June 1998 , pp. 166 - 177
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. van den Berg, J. and Keane, M., On the continuity of the percolation function. In: Conference on Modern Analysis and Probability (Eds. R. Beals et al.). Contemp. Math. 26 (1984), 61–65.Google Scholar
2. de Bruijn, N. G., Algebraic theory of Penrose's non-periodic tilings of the plane. I. Nederl. Akad. Wetensch. Indag. Math. 84 (1981), 39–52.Google Scholar
3. de Bruijn, N. G., Algebraic theory of Penrose's non-periodic tilings of the plane. II. Nederl. Akad. Wetensch. Indag. Math. 84 (1981), 53–66.Google Scholar
4. de Bruijn, N. G., Updown generation of Penrose tilings. Indag. Math. (N.S.) 1 (1990), 201–220.Google Scholar
5. Burton, R. M. and Keane, M., Density and uniqueness in percolation. Commun. Math. Phys. 121 (1989), 501–505.Google Scholar
6. Fortuin, C. M., Ginibre, J., and Kasteleyn, P. W., Correlation inequalities on some partially ordered sets. Commun. Math. Phys. 22 (1971), 89–103.Google Scholar
7. Gandolfi, A., Keane, M. S., and Newman, C. M., Uniqueness of the infinite component in a random graph with applications to percolation and spin glasses. Probab. Theory Related Fields 92 (1992), 511–527.Google Scholar
8. Geerse, C. P. M. and Hof, A., Lattice gas models on self-similar aperiodic tilings. Rev. Math. Phys. 3 (1991), 163–221.Google Scholar
9. Grimmett, G., Percolation. Springer, 1989.Google Scholar
10. Gr ünbaum, B. and Shephard, G. C., Tilings and Patterns. W. H. Freeman and Company, 1987.Google Scholar
11. Hof, A., Some remarks on discrete aperiodic Schrödinger operators. J. Stat. Phys. 72 (1993), 1353–1374.Google Scholar
12. Hof, A., On diffraction by aperiodic structures. Commun. Math. Phys. 169 (1995), 25–43.Google Scholar
13. Lu, Jian Ping and Birman, J. L., Percolation and scaling on a quasilattice. J. Stat. Phys. 46 (1987), 1057–1066.Google Scholar
14. Katz, A. and Duneau, M., Quasiperiodic patterns and icosahedral symmetry. J. Physique 47 (1986), 181–196.Google Scholar
15. Kesten, H., Percolation Theory for Mathematicians. Birkhäuser, 1982.Google Scholar
16. Lunnon, W. F. and Pleasants, P. A. B., Quasicrystallographic tilings. J. Math. Pures Appl. 66 (1987), 217–263.Google Scholar
17. Menshikov, M. V., Coincidence of critical points in percolation problems. Soviet Math. Dokl. 33 (1986), 856–869.Google Scholar
18. Newman, C. M. and Schulman, L. S., Infinite clusters in percolation models. J. Stat. Phys. 26 (1981), 613–628.Google Scholar
19. Preston, C. J., Gibbs States on Countable Sets. Cambridge University Press, 1974.Google Scholar
20. Radin, C. and Wolf, M., Space tilings and local isomorphism. Geom. Dedicata 42 (1992), 355–360.Google Scholar
21. Robinson, E. A. Jr., The dynamical properties of Penrose tilings. Trans. Amer. Math. Soc. 348 (1996), 4447–4469.Google Scholar
22. Rudolph, D. J., Rectangular tilings of Rn and free Rn actions. Lecture Notes in Math. 1342 (1988), 653–689.Google Scholar
23. Sakamoto, S., Yonezawa, F., Aoki, K., Nosé, S., and Hori, M., Percolation in two-dimensional quasicrystals by Monte Carlo simulations. J. Phys. A 22(1989), L705–L709.Google Scholar
24. Shechtman, D., Blech, I., Gratias, D., and Cahn, J. W., Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 53 (1984), 1951–1953.Google Scholar
25. Solomyak, B., Dynamics of self-similar tilings. Ergodic Theory Dynamical Systems, to appear.Google Scholar
26. Walters, P., An Introduction to Ergodic Theory. Springer Verlag, 1982.Google Scholar
27. Yonezawa, F. et al., Percolation in Penrose tiling and its dual—in comparison with analysis for Kagomé, dice and square lattices. J. Non-Cryst. Solids 106 (1988), 262–269.Google Scholar