Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T13:06:35.051Z Has data issue: false hasContentIssue false
  • English
  • Français

Perfect Non-Extremal Riemann Surfaces

Published online by Cambridge University Press:  20 November 2018

Paul Schmutz Schaller
Paul Schmutz Schaller*
Affiliation:
Université de Neuchâtel Institut de mathématiques Rue Emile-Argand 11 CH-2007 Neuchâtel Switzerland, Paul.Schmutz@maths.unine.ch
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An infinite family of perfect, non-extremal Riemann surfaces is constructed, the first examples of this type of surfaces. The examples are based on normal subgroups of the modular group 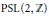$\text{PSL}\left( 2,\,\mathbb{Z} \right)$ of level 6. They provide non-Euclidean analogues to the existence of perfect, non-extremal positive definite quadratic forms. The analogy uses the function syst which associates to every Riemann surface 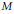$M$ the length of a systole, which is a shortest closed geodesic of 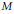$M$.

Keywords

11H9911F0630F45
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 1 , 01 March 2000 , pp. 115 - 125
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Ash, A., On eutactic forms. Canad. J. Math. 29 (1977), 1040–1054.Google Scholar
[2] Barnes, E. S., The perfect and extreme senary forms. Canad. J. Math. 9 (1957), 235–242.Google Scholar
[3] Barnes, E. S., The complete enumeration of extreme senary forms. Philos. Trans. Roy. Soc. London Ser. A 249 (1957), 461–506.Google Scholar
[4] Bavard, C., Systole et invariant d’Hermite. J. Reine Angew.Math. 482 (1997), 93–120.Google Scholar
[5] Buser, P., Geometry and spectra of compact Riemann surfaces. Birkhäuser, 1992.Google Scholar
[6] Conway, J. H. and Sloane, N. J. A., Low-dimensional lattices, III. Perfect forms. Proc. Roy. Soc. London Ser. A 118 (1988), 43–80.Google Scholar
[7] Conway, J. H. and Sloane, N. J. A., Sphere packings, lattices and groups. Second ed., Springer, 1993.Google Scholar
[8] Coxeter, H. S. M., Extreme forms. Canad. J. Math. 3 (1951), 391–441.Google Scholar
[9] Coxeter, H. S. M. and Moser, W. O. J., Generators and relations for discrete groups. Fourth ed., Springer, 1980.Google Scholar
[10] Gruber, P. M. and Lekkerkerker, C. G., The geometry of numbers. Second ed., North-Holland, 1987.Google Scholar
[11] Kerckhoff, S., The Nielsen realization problem. Ann. of Math. 117 (1983), 235–265.Google Scholar
[12] Luo, W., Rudnick, Z. and Sarnak, P., On Selberg's eigenvalue conjecture. Geom. Funct.Anal. 5 (1995), 387–401.Google Scholar
[13] Martinet, J., Les réseaux parfaits des espaces euclidiens. Masson, Paris, 1996.Google Scholar
[14] Newman, M., Integral matrices. Academic Press, 1972.Google Scholar
[15] Quine, J. R. and P. Sarnak (eds.), Extremal Riemann surfaces. Contemp. Math. 201, Amer.Math. Soc., 1997.Google Scholar
[16] Quine, J. R. and Zhang, P. L., Extremal symplectic lattices. Israel J. Math. (to appear).Google Scholar
[17] Schmutz, P., Die Parametrisierung des Teichmüllerraumes durch geodätische Längenfunktionen. Comment. Math. Helv. 68 (1993), 278–288.Google Scholar
[18] Schmutz, P., Riemann surfaces with shortest geodesic of maximal length. Geom. Funct. Anal. 3 (1993), 564–631.Google Scholar
[19] Schmutz, P., Systoles on Riemann surfaces. Manuscripta Math. 85 (1994), 429–447.Google Scholar
[20] Schmutz Schaller, P., Systole is a topological Morse function for Riemann surfaces. Preprint, 1997.Google Scholar
[21] Schmutz Schaller, P., Geometry of Riemann surfaces based on closed geodesics. Bull. Amer.Math. Soc. 35 (1998), 193–214.Google Scholar
[22] Voronoï, G., Sur quelques propriétés des formes quadratiques positives parfaites. J. Reine Angew. Math. 133 (1908), 97–178.Google Scholar
[23] Zograf, P. G., Small eigenvalues of automorphic Laplacians in spaces of parabolic forms. J. Soviet Math. 36 (1987), 106–114.Google Scholar