Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T13:37:02.343Z Has data issue: false hasContentIssue false
  • English
  • Français

Poincaré Lemma on Quaternion-like Heisenberg Groups

Published online by Cambridge University Press:  20 November 2018

Der-Chen Chang ,
Nanping Yang  and
Hsi-Chun Wu
Der-Chen Chang
Affiliation:
Department of Mathematics and Statistics, Georgetown University, Washington D.C. 20057, USA, e-mail : chang@georgetown.edu Department of Mathematics, Fu Jen Catholic University, Taipei 242, Taiwan, ROC, e-mail : yang@math.fju.edu.tw
Nanping Yang
Affiliation:
Department of Mathematics and Statistics, Georgetown University, Washington D.C. 20057, USA, e-mail : chang@georgetown.edu Department of Mathematics, Fu Jen Catholic University, Taipei 242, Taiwan, ROC, e-mail : yang@math.fju.edu.tw
Hsi-Chun Wu
Affiliation:
Graduate Institute of Applied Science and Engineering, Fu Jen Catholic University, Taipei 242, Taiwan, ROC, e-mail : 400068060@mail.fju.edu.tw
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For smooth functions 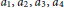${{a}_{1}}\,,\,{{a}_{2}}\,,\,{{a}_{3}}\,,\,{{a}_{4}}\,$ on a quaternion Heisenberg group, we characterize the existence of solutions of the partial differential operator system 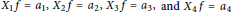${{X}_{1}}f\,=\,{{a}_{1}},\,{{X}_{2}}f=\,{{a}_{2}},\,{{X}_{3}}f\,=\,{{a}_{3}},\,\text{and}\,{{X}_{4}}f\,=\,{{a}_{4}}$. In addition, a formula for the solution function 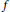$f$ is deduced, assuming solvability of the system.

Keywords

93B0549N99bracket generating propertyquaternion Heisenberg groupcurlintegrability conditionPoincaré lemma
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 3 , 01 September 2018 , pp. 495 - 508
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Calin, O., Chang, D. C., and Eastwood, M., Integrability conditions for Heisenberg and Grushin-type distributions. Anal. Math. Phys. 4(2014), no. 1-2, 99–114. http://dx.doi.Org/10.1007/s13324-014-0073-1Google Scholar
[2] Calin, O., Chang, D. C., and Hu, J., Poincare's lemma on the Heisenberg group. Adv. in Appl. Math. 60(2014), 90–102. http://dx.doi.org/10.101 6/j.aam.2014.08.003Google Scholar
[3] Chang, D. C., Markina, I., and Wang, W., On the Cauchy-Szegö kernet for quaternion Siegel upper half-space. Complex Anal. Oper. Theory 7(2013), no. 5, 1623–1654. http://dx.doi.Org/10.1007/s11785-012-0282-2Google Scholar
[4] Chow, W.-L., Über Systeme von linearen partiellen Differentialgleichungen erster Ordnung. Math. Ann. 117(1939), 98–105. http://dx.doi.Org/10.1007/BF01450011Google Scholar
[5] Fefferman, C. and Phong, D. H., The uncertainty principle and sharp Garding inequalities. Comm. Pure and Applied Math. 34(1981), 285–331. http://dx.doi.org/10.1002/cpa.3160340302Google Scholar
[6] Hörmander, L., Hypoelliptic second order differential equations. Acta Math. 119(1967), 147–171. http://dx.doi.org/10.1007/BF02392081Google Scholar
[7] Wang, W., The tangential Cauchy-Fueter complex on the quaternionic Heisenberg group. J. Geom. Phys. 61(2011), 363–380. http://dx.doi.Org/10.1016/j.geomphys.2010.10.006Google Scholar