Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T06:04:02.405Z Has data issue: false hasContentIssue false
  • English
  • Français

A Pólya–Vinogradov inequality for short character sums

Part of: Exponential sums and character sums

Published online by Cambridge University Press:  02 December 2020

Matteo Bordignon
Matteo Bordignon*
Affiliation:
School of Science, University of New South Wales Canberra, Canberra, Australia
*
e-mail:m.bordignon@student.unsw.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we obtain a variation of the Pólya–Vinogradov inequality with the sum restricted to a certain height. Assume 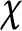$\chi $ to be a primitive character modulo q, 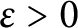$ \epsilon>0$ and 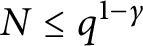$N\le q^{1-\gamma }$ , with 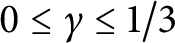$0\le \gamma \le 1/3$ . We prove that

$$ \begin{align*} |\sum_{n=1}^N \chi(n) |\le c (\tfrac{1}{3} -\gamma+\epsilon )\sqrt{q}\log q \end{align*} $$
with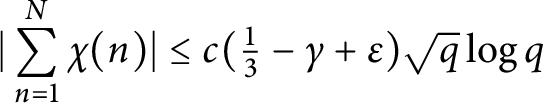 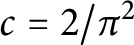$c=2/\pi ^2$ if 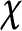$\chi $ is even and 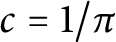$c=1/\pi $ if 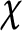$\chi $ is odd. The result is based on the work of Hildebrand and Kerr.

Keywords

Character sumsPólya-Vinogradov inequality

MSC classification

Primary: 11L05: Gauss and Kloosterman sums; generalizations
Secondary: 11L40: Estimates on character sums
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 4 , December 2021 , pp. 906 - 910
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bober, J., Goldmakher, L., Granville, A., and Koukoulopoulos, D., The frequency and the structure of large character sums . J. Eur. Math. Soc. (JEMS) 20(2018), 1759–1818. https://doi.org/10.4171/JEMS/799 CrossRefGoogle Scholar
Bordignon, M., Partial Gaussian sums and the Pólya–Vinogradov inequality for primitive characters. Preprint, 2020. arXiv:2001.05114 CrossRefGoogle Scholar
Bordignon, M. and Kerr, B., An explicit Pólya–Vinogradov inequality via Partial Gaussian sums . Trans. Amer. Math. Soc. 373(2020), 6503–6527. https://doi.org/10.1090/tran/8138 CrossRefGoogle Scholar
Kerr, B., On the constant in the Pólya-Vinogradov inequality . J. Number Theory 212(2020), 265–284. https://doi.org/10.1016/j.jnt.2019.11.003 CrossRefGoogle Scholar
Frolenkov, D. A. and Soundararajan, K., A generalization of the Pólya-Vinogradov inequality . Ramanujan J. 31(2013), 271–279. https://doi.org/10.1007/s11139-012-9462-y CrossRefGoogle Scholar
Granville, A. and Soundararajan, K., Large character sums: pretentious characters and the Pólya-Vinogradov theorem . J. Amer. Math. Soc. 20(2007), 357–384. https://doi.org/10.1090/S0894-0347-06-00536-4 CrossRefGoogle Scholar
Hildebrand, A., On the constant in the Pólya-Vinogradov inequality . Canad. Math. Bull. 31(1988), 347–352. https://doi.org/10.4153/CMB-1988-050-1 Google Scholar
Hildebrand, A., Large values of character sums . J. Number Theory 29(1988), 271–296. https://doi.org/10.1016/0022-314X(88)90106-0 CrossRefGoogle Scholar
Pólya, G. and Szegö, G., Problems and theorems in analysis. II. Springer-Verlag, Berlin, Heidelberg, 1998.CrossRefGoogle Scholar
Pomerance, C., Remarks on the Pólya-Vinogradov inequality . Integers 11(2011), 531–542. https://doi.org/10.1515/integ.2011.039 CrossRefGoogle Scholar
Young, W. H., On a certain series of Fourier . Proc. Lond. Math. Soc. (2) 11(1913), 357–366. https://doi.org/10.1112/plms/s2-11.1.357 CrossRefGoogle Scholar