Positive Definite Distributions and Subspaces of L__p With Applications to Stable Processes

Abstract

We define embedding of an $n$-dimensional normed space into 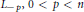${{L}_{-p}},\,0\,<\,p\,<\,n$ by extending analytically with respect to 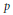$p$ the corresponding property of the classical 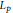${{L}_{p}}$-spaces. The well-known connection between embeddings into 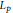${{L}_{p}}$ and positive definite functions is extended to the case of negative 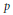$p$ by showing that a normed space embeds in 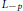${{L}_{-p}}$ if and only if 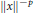$\parallel x{{\parallel }^{-p}}$ is a positive definite distribution. We show that the technique of embedding in 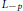${{L}_{-p}}$ can be applied to stable processes in some situations where standard methods do not work. As an example, we prove inequalities of correlation type for the expectations of norms of stable vectors. In particular, for every 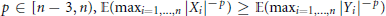$P\in [n-3,n),\mathbb{E}({{\max }_{i=1,...,n}}{{\left| {{X}_{i}} \right|}^{-p}})\ge \mathbb{E}({{\max }_{i=1,...,n}}{{\left| {{Y}_{i}} \right|}^{-p}})$, where 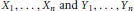${{X}_{1}},...,{{X}_{n}}\,\text{and}\,{{Y}_{1}},...,{{Y}_{n}}$ are jointly 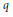$q$-stable symmetric random variables, 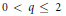$0\,<\,q\,\le \,2$, so that, for some 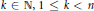$k\,\in \,\mathbb{N},\,1\,\le \,k\,<\,n$, the vectors 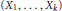$\left( {{X}_{1}},\,.\,.\,.\,,\,{{X}_{k}} \right)$ and 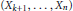$\left( {{X}_{k+1}},\,.\,.\,.\,,{{X}_{n}} \right)$ have the same distributions as 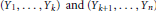$({{Y}_{1}},...,{{Y}_{k}})\,\,\text{and}\,\,({{Y}_{k+1}},...,{{Y}_{n}})$, respectively, but 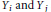${{Y}_{i}}\,\text{and}\,{{Y}_{j}}$ are independent for every choice of 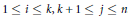$1\,\le \,i\,\le \,k,\,k\,+\,1\,\le \,j\,\le \,n$.