Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T16:32:11.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Prime and Primary Ideals in a Prüfer Order in a Simple Artinian Ring with Finite Dimension over its Center

Published online by Cambridge University Press:  20 November 2018

H. Marubayashi  and
A. Ueda
H. Marubayashi
Affiliation:
Department of Mathematics Naruto University of Education Naruto, Tokushima 772-8502 Japan
A. Ueda
Affiliation:
Department of Mathematics Shimane University Matsue, Shimane 690-8504 Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 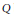$Q$ be a simple Artinian ring with finite dimension over its center. An order 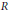$R$ in 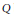$Q$ is said to be Prüfer if any one-sided 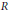$R$-ideal is a progenerator. We study prime and primary ideals of a Prüfer order under the condition that the center is Prüfer. Also we characterize branched and unbranched prime ideals of a Prüfer order.

Keywords

16H0516L30
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 3 , 01 September 1999 , pp. 371 - 379
Copyright
Copyright © Canadian Mathematical Society 1999

References

[AD] Alajbegovi`c, J. H. and Dubrovin, N. I., Non-commutative Prüfer rings. J. Algebra 135 (1990), 165–176.Google Scholar
[D1] Dubrovin, N. I., Noncommutative valuation rings. Trans. MoscowMath. Soc. 45 (1984), 273–287.Google Scholar
[D2] Dubrovin, N. I., Noncommutative valuation ring in simple finite-dimensional algebras over a field.Math. USSRSb. (2) 51 (1985), 493–505.Google Scholar
[D3] Dubrovin, N. I., Noncommutative Prüfer rings. Math. USSR-Sb. 74 (1993), 1–8.Google Scholar
[Gi] Gilmer, R., Multiplicative Ideal Theory. Marcel Dekker Inc., New York, 1972.Google Scholar
[G1] Gräter, J., The defectsatz for central simple algebras. Trans. Amer.Math. Soc. (2) 330 (1992), 823–843.Google Scholar
[G2] Gräter, J., Prime PI rings in which finitely generated right ideals are principal. Math. Forum 4 (1992), 447–463.Google Scholar
[H] Hutchins, H. C., Examples of Commutative Rings. Polygonal Publishing House, 1981.Google Scholar
[L] Lambek, J., Lectures on rings and modules. Chelsea Publishing Company, New York, 1986.Google Scholar
[MMU] Marubayashi, H., Miyamoto, H. and Ueda, A., Prime ideals in noncommutative valuation rings in finite dimensional central simple algebras. Proc. Japan Acad. Ser. A Math. Sci. (2) 69 (1993), 35–40.Google Scholar
[MM1] Marubayashi, H., Miyamoto, H., Ueda, A. and Zhao, Y., Semi-hereditary orders in a simple Artinian ring. Comm. Algebra (13) 22 (1994), 5209–5230.Google Scholar
[MM2] Marubayashi, H., Miyamoto, H., Ueda, A. and Zhao, Y., On semi-local Bezout orders and strongly Prüfer orders in a central simple algebra. Math. Japon. (2) 43 (1996), 377–382.Google Scholar
[MY] Marubayashi, H. and Yi, Z., Dubrovin valuation properties of skew group rings and crossed products. Comm. Algebra, to appear.Google Scholar
[M1] Morandi, P. J., Maximal orders over valuation ring. J. Algebra 152 (1992), 313–341.Google Scholar
[M2] Morandi, P. J., Noncommutative Prüfer rings satisfying a polynomial identity. J. Algebra 161 (1993), 324–341.Google Scholar