Projective freeness and stable rank of algebras of complex-valued BV functions

Abstract

The paper investigates the algebraic properties of weakly inverse-closed complex Banach function algebras generated by functions of bounded variation on a finite interval. It is proved that such algebras have Bass stable rank 1 and are projective-free if they do not contain nontrivial idempotents. These properties are derived from a new result on the vanishing of the second Čech cohomology group of the polynomially convex hull of a continuum of a finite linear measure described by the classical H. Alexander theorem.

1 Formulation of main results

1.1

Let $BV(I)$ be the space of complex-valued functions of bounded variation on the interval $I=[a,b]$ . By definition, $f\in BV(I)$ if and only if

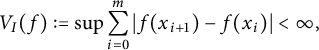(1.1) $$ \begin{align} V_I(f):=\sup \sum_{i=0}^m|f(x_{i+1})-f(x_i)|<\infty, \end{align} $$

where the supremum is taken over all partitions $a=x_0<x_1<\cdots <x_m=b$ , $m\in \mathbb {N}$ , of I. In this paper, we study algebraic properties of weakly inverse-closed complex Banach function algebras generated by $BV(I)$ functions. Here, by a complex Banach function algebra, we mean a unital subalgebra A of the algebra of complex-valued functions on a set X with pointwise sum and product equipped with a norm that makes A a Banach algebra. Such an algebra A is called weakly inverse-closed if it satisfies the condition:

1. (wi) If $f\in A$ , and $\sup _{X}|f(x)|<1$ , then $\frac {1}{1-f}\in A$ .

To formulate the results, recall that a unital commutative ring R is said to be projective free if every finitely generated projective R-module is free (i.e., if M is an R-module such that $M\oplus N\cong R^n$ for an R-module N and $n \in \mathbb {Z} _+\, (:= \mathbb {N}\cup \{0\})$ , then $M\cong R^m$ for some $m \in \mathbb {Z} _+$ ). Let $M_n(R)$ denote the ring of $n\times n$ matrices over R and $GL_n(R)$ its unit group. In terms of matrices, the ring R is projective-free if and only if for each $n\in \mathbb {N}$ , every $X\in M_n(R)\setminus \{0_n, I_n\}$ such that $X^2=X$ (i.e., an idempotent) has a form $X=S(I_r\oplus 0_{n-r})S^{-1}$ for some $ S\in GL_n(R)$ , $r\in \{1,\dots , n-1\}$ ; here, $0_k$ and $I_k$ are zero and identity matrices in $M_k(R)$ (see [9, Proposition 2.6]). (For some examples of projective-free rings and their applications, see, e.g., [8, 17, 25] and the references therein.)

Let $A\subset \ell ^{\infty }(I)$ be a weakly inverse-closed complex Banach function algebra such that the subalgebra $A\cap BV(I)$ is dense in A. We denote by $1_I$ the unit of A (i.e., the constant function of value $1$ on I). For a nonzero idempotent $p\in A$ , we set $A_p:=\{pg\, :\, g\in A\}$ . Then $A_p$ is a closed subalgebra of A with unit p. If M is an A-module, then $M_p:=\{pm\, :\, m\in M\}$ is a submodule which can be regarded as an $A_p$ -module as its annihilator contains $\mathrm {ker}\,(1_I-p)$ .

Theorem 1.1 Let M be a finitely generated projective A-module. Then there exist idempotents $p_1,\dots , p_k\in A$ such that $M=\oplus _{i=1}^k\, M_{p_i}$ and each $M_{p_i}$ is a free $A_{p_i}$ -module. In particular, if $A\subset C(I)$ , then it is a projective-free ring.

For instance, Theorem 1.1 holds true for weakly inverse-closed complex Banach function algebras $A\subset BV(I)$ and their uniform closures $\bar A\subset \ell ^{\infty }(I)$ .

In terms of matrices, Theorem 1.1 asserts that for every idempotent $X\in M_n(A)$ , $n\in \mathbb {N}$ , there exist idempotents $p_1,\dots , p_k\in A$ with $\sum _{j=1}^k p_j=1$ and $I_1,\dots , I_k\in M_n({\mathbb C})$ , $k\in \mathbb {N}$ , and an invertible matrix $G\in GL_n(A)$ such that $G^{-1}XG=\sum _{j=1}^k p_jI_j$ (see Section 4 for an operator-valued generalization of this result).

Let A be an associative ring with unit. For a natural number n, let $U_n(A)$ denote the set of unimodular elements of $A^n$ , i.e.,

$$\begin{align*}U_n(A)=\left\{(a_1,\dots, a_n)\in A^n\, :\, Aa_1+\cdots +Aa_n=A\right\}. \end{align*}$$

An element $(a_1,\dots , a_n)\in U_n(A)$ is called reducible if there exist $c_1,\dots , c_{n-1}\in A$ such that $(a_1+c_1 a_n,\dots , a_{n-1}+c_{n-1}a_n)\in U_{n-1}(A).$ The stable rank of A is the least n such that every element of $U_{n+1}(A)$ is reducible. The concept of the stable rank introduced by Bass [2] plays an important role in some stabilization problems of algebraic K-theory. Following Vaserstein [24], we call a ring of stable rank $1$ a B-ring. (We refer to this paper for some examples and properties of B-rings.)

Theorem 1.2 Each weakly inverse-closed complex Banach function algebra ${A\subset BV(I)}$ is a B-ring.

Example 1.3 Since every closed unital subalgebra of a weakly inverse-closed complex Banach function algebra is weakly inverse-closed (see Lemma 2.1), Theorems 1.1 and 1.2 are applicable to closed unital subalgebras of the following weakly inverse-closed function algebras: (a) $(BV(I),\lVert \cdot \rVert _{BV})$ , where $\lVert f\rVert _{BV}:=\sup _{I}|f|+V_I(f)$ ; (b) $(AC(I),\lVert \cdot \rVert _{AC})$ —the algebra of absolutely continuous complex-valued functions on I, where $\|f\|_{AC}:=\max _I |f|+\int _I\, |f'(t)|\,dt$ ; (c) $(\mathrm {Lip}(I),\lVert \cdot \rVert _{\mathrm {Lip}})$ —the algebra of complex-valued Lipschitz functions on I, where $\|f\|_{\mathrm {Lip}}:=\max _I |f|+\sup _{x\ne y}\frac {|f(x)-f(y)|}{|x-y|}$ ; and (d) $(C^k(I),\lVert \cdot \rVert _{C^k})$ —the algebra of complex-valued $C^k$ functions on I, $k\ge 1$ , where $\|f\|_{C^k}:=\sum _{i=0}^k \max _I |f^{(i)}|$ .

1.2

Theorems 1.1 and 1.2 are derived from a general result presented in this section. For its formulation, recall that for a commutative unital complex Banach algebra A, the maximal ideal space $\mathfrak M(A)\subset A^{\ast }$ is the set of nonzero homomorphisms $A \!\rightarrow \! {\mathbb C}$ endowed with the Gelfand topology, the weak- $\ast $ topology of $A^{\ast }$ . It is a compact Hausdorff space contained in the unit sphere of $A^{\ast }$ . The Gelfand transform defined by $\hat {a}(\varphi ):=\varphi (a)$ for $a\in A$ and $\varphi \in \mathfrak M(A)$ is a nonincreasing-norm morphism from A into $C(\mathfrak M (A))$ , the Banach algebra of complex-valued continuous functions on $\mathfrak M(A)$ . Also, recall that the covering dimension of a topological space X, denoted by $\mathrm {dim}\, X$ , is the smallest integer d such that every open cover of X has an open refinement of order at most $d+1$ . If no such integer exists, then X is said to have infinite covering dimension.

Theorem 1.4 Let $A\subset \ell ^{\infty }(I)$ be a weakly inverse-closed complex Banach function algebra such that $A\cap BV(I)$ is dense in A. Then $\mathrm {dim}\,\mathfrak M(A)\le 2$ and the Čech cohomology group $H^2(\mathfrak M(A),\mathbb {Z} )=0$ .

Note that for a weakly inverse-closed complex Banach function algebra $A\subset \ell ^{\infty }(I)$ with uniform closure $\bar A$ , the maximal ideal spaces $\mathfrak M(A)$ and $\mathfrak M(\bar A)$ are homeomorphic (see, e.g., [19, Proposition 3]).

Example 1.5 (1) As a Banach algebra, $BV(I)=\ell ^1(I)\rtimes BV_+(I)$ —the semidirect product of the closed ideal $\ell ^1(I)$ and the Banach subalgebra $BV_+(I)$ of right-continuous $BV$ functions (see, e.g., [6, Corollary 2.2]). Thus, the uniform closure $\overline {BV(I)}=c_0(I)\rtimes R_+(I)$ —the semidirect product of the closed ideal $c_0(I)$ of functions with at most countable supports converging to $0$ and the Banach subalgebra ${R_+(I)\subset \ell ^{\infty }(I)}$ of right-continuous functions having first kind discontinuities. Then each homomorphism in $\mathfrak M(\overline {BV(I)})$ is uniquely determined by its restrictions to $c_0(I)$ and $R_+(I)$ . This leads to a continuous injection $r:\mathfrak M(\overline {BV(I)})\to \mathfrak M(c(I))\times \mathfrak M(R_+(I))$ , where $c(I):={\mathbb C}\cdot 1_I\oplus c_0(I)$ . Next, $\mathfrak M(c(I))$ is homeomorphic to the one-pointed compactification of the discrete set I. In particular, $\mathrm {dim}\,\mathfrak M(c(I))=0$ . In turn, there is a continuous surjection $p: \mathfrak M(R_+(I))\to \mathfrak M(C(I))=I$ , the transpose of the embedding $C(I)\hookrightarrow R_+(I)$ , whose fibres consist of two points over interior points of I and of one point over the endpoints of I. (Specifically, if $\varphi \in p^{-1}(x)$ , then $\varphi (f)$ is equal either to $f(x^-)$ or to $f(x^+)$ .) Moreover, $\mathrm {dim}\,\mathfrak M(R_+(I))=0$ (see, e.g., [7, Theorem 1.7]). These imply that r embeds $\mathfrak M(\overline {BV(I)})$ into the zero-dimensional compact Hausdorff space $\mathfrak M(c(I))\times \mathfrak M(R_+(I))$ ; hence, $\mathrm {dim}\,\mathfrak M(BV(I))=\mathrm { dim}\,\mathfrak M(\overline {BV(I)})=0$ and $H^i(\mathfrak M(BV(I)),\mathbb {Z} )=0$ for all $i\in \mathbb {N}$ .

(2) If A is one of the algebras (b),(c), or (d) of Example 1.3, then $\mathfrak M(\bar A)$ is homeomorphic to I and, hence, $\mathrm {dim}\, \mathfrak M(\bar A)=1$ and $H^i(\mathfrak M(\bar A),\mathbb {Z} )=0$ for all $i\in \mathbb {N}$ .

(3) If A is a weakly inverse-closed algebra generated by $f_1,\dots , f_n\in BV(I)$ , then $\mathfrak M(A)$ is homeomorphic to the polynomially convex hull of the range of $(f_1,\dots , f_n): I\to {\mathbb C}^n$ described by the Alexander theorem [1] presented in the next section (see, e.g., [19, Proposition 1] and [14, Chapter III, Theorem 1.4]).

1.3

In the sequel, $\mathscr H^1$ denotes the Hausdorff one-dimensional measure. Furthermore,

$$\begin{align*}\widehat{K}:=\bigl\{z\in{\mathbb C}^n\, :\, |p(z)|\le \sup\nolimits_{K}\,|p|\quad \forall p\in{\mathbb C} [z_1,\dots, z_n]\bigr\} \end{align*}$$

stands for the polynomially convex hull of a bounded subset $K\subset {\mathbb C}^n$ . If $X\Subset {\mathbb C}^n$ , then $P(X)\subset C(X)$ denotes the uniform closure of the restriction of polynomials ${\mathbb C} [z_1,\dots , z_n]|_X$ . A compact connected subset of ${\mathbb C}^n$ is called a continuum.

The following result is due to Alexander [1, Theorem 1].

Theorem A Suppose that $\Gamma \subset {\mathbb C}^n$ is a compact subset of a continuum of finite $\mathscr H^1$ -measure. Then $\widehat {\Gamma }\setminus \Gamma $ is a (possibly empty) pure one-dimensional complex analytic subset of ${\mathbb C}^n\setminus \Gamma $ . If $H^1(\Gamma ,\mathbb {Z} )=0$ , then $\widehat \Gamma =\Gamma $ and $P(\Gamma )=C(\Gamma )$ .

For historical remarks and further developments related to this theorem, see [21].

Using Theorem A, we prove the following.

Theorem 1.6 Suppose that $\Gamma \subset {\mathbb C}^n$ is a compact subset of a continuum of finite $\mathscr H^1$ -measure. Then (a) $\mathrm {dim}\,\widehat \Gamma \le 2$ and (b) $H^2(\widehat \Gamma ,\mathbb {Z} )=0$ .

Theorem 1.6 describes the algebraic–topological structure of the polynomial convex hull in the Alexander theorem and fills a gap in this area of study. Theorem 1.4 is derived from Theorem 1.6.

The proof of Theorem 1.6 goes along the following lines. Part (a) of the theorem follows from Theorem A by virtue of some standard results of dimension theory. Then, using that a continuum with finite $\mathscr H^1$ -measure in ${\mathbb C}^n$ is contained in a rectifiable curve (see, e.g., [13, Chapter 3]), part (b) of the theorem reduces to a similar result for the cohomology of the maximal ideal space $\mathfrak M(A)$ of a closed finitely generated subalgebra $A\subset \mathrm {Lip}(I)$ . Each such A is weakly inverse-closed. Therefore, $\mathfrak M(A)$ is homeomorphic to the polynomially convex hull of a rectifiable curve in some ${\mathbb C}^n$ which is the image of I under the map $I\to {\mathbb C}^n$ whose coordinates are generators of A. Then, part (a) of the theorem implies that $\mathrm {dim}\,\mathfrak M(A)\le 2$ . In turn, due to the Novodvorskii–Taylor theory [23], to prove that $H^2(\mathfrak M(A),\mathbb {Z} )=0$ under the condition $\mathrm {dim}\,\mathfrak M(A)\le 2$ , one must show that $2\times 2$ matrix idempotents of rank $1$ with entries in A are similar over A to constant idempotents. The space of such idempotents over ${\mathbb C}$ is a two-dimensional complex algebraic subvariety of ${\mathbb C}^4$ of the form $X_1\sqcup X_2\sqcup X_3$ such that $X_1\cong X_2\cong {\mathbb C}$ and the projection ${\mathbb C}^4\to {\mathbb C}^2$ onto the first two coordinates is constant along $X_1$ and $X_2$ and maps $X_3$ biholomorphically onto ${\mathbb C}\times {\mathbb C}^*$ , where ${\mathbb C}^*:={\mathbb C}\setminus \{0\}$ . Using this, Theorem A, and part (a) of the theorem, we deduce that $H^2(\mathfrak M(A),\mathbb {Z} )=0$ from the known result on the vanishing of two cohomology of a polynomially convex subset of ${\mathbb C}^2$ (see, e.g., [21, Chapter 2.3]).

2 Proof of Theorem 1.6

(a) Let $\mathrm {dim}_{\mathscr H}$ denote the Hausdorff dimension. By the Szpilrajn theorem (see, e.g., [15, pp. 62–63]) and because $\mathscr H^1(\Gamma )<\infty $ ,

(2.1) $$ \begin{align} \mathrm{dim}\,\Gamma\le \mathrm{dim}_{\mathscr H}\Gamma=1. \end{align} $$

In turn, as $\widehat \Gamma \setminus \Gamma \ne \emptyset $ is a one-dimensional complex analytic space, its compact subsets have covering dimension $\le 2$ . These imply that $\mathrm {dim}\,\widehat \Gamma \le 2$ (see, e.g., [18, Chapter 2, Theorems 9–11]).

(b) In the proof, we use the following results.

Lemma 2.1 Let A be a weakly inverse-closed complex Banach function algebra on a set X. Then every closed unital subalgebra $B\subset A$ is weakly inverse-closed.

Proof Suppose that $f\in B$ is such that $\sup _X |f|<1$ . Since the algebra $ A$ is weakly inverse-closed, $\frac {1}{1-f}\in A$ . Also, the function $\frac {1}{1-f}$ is the sum of the uniformly convergent on X series $\sum _{k=0}^{\infty } f^k$ . By the formula for the spectral radius of f (see, e.g., [14, Chapter I, Theorem 5.2]),

(2.2) $$ \begin{align} \sup_{\mathfrak M( A)}|\hat f|=\lim_{k\to\infty}\|f^k\|^{\frac 1 k}; \end{align} $$

here, $\hat {f}$ is the Gelfand transform of f and $\lVert\cdot\rVert$ is the norm on $ A$ .

On the other hand, since $ A$ is weakly inverse-closed, [19, Proposition 1] implies that

(2.3) $$ \begin{align} \sup_{\mathfrak M( A)}|\hat f|= \sup_X |f|. \end{align} $$

Combining (2.2) and (2.3), we get for some $c\in (\sup _X |f|, 1)$ and all sufficiently large $k\in \mathbb {N}$ ,

(2.4) $$ \begin{align} \|f^k\|\le c^k. \end{align} $$

This shows that the partial sums of the series $\sum _{k=0}^{\infty } f^k$ form a Cauchy sequence in $ A$ . Since these partial sums belong to the closed subalgebra $B\subset A$ , the series converges to an element of B. This implies that $\frac {1}{1-f}\in B$ , as required.

Proposition 2.2 Suppose that $\mathcal A$ is a complex Banach function algebra defined on its maximal ideal space $\mathfrak M(\mathcal A)$ . If $\mathrm {dim}\,\mathfrak M(\mathcal A)\le 2$ , then there are bijections:

1. (a) $c_1:\mathrm {Vect}_1(\mathfrak M(\mathcal A))\to H^2(\mathfrak M(\mathcal A),\mathbb {Z} )$ , where $\mathrm {Vect}_1(\mathfrak M(\mathcal A))$ is the set of isomorphism classes of complex rank-1 vector bundles over $\mathfrak M(\mathcal A)$ .

2. (b) $h: [\mathfrak M(\mathcal A),\mathbb S^2]\to H^2(\mathfrak M(\mathcal A),\mathbb {Z} )$ , where $[\mathfrak M(\mathcal A),\mathbb S^2]$ is the set of homotopy classes of continuous maps from $\mathfrak M(\mathcal A)$ to the two-dimensional unit sphere $\mathbb S^2$ .

3. (c) $i:[\mathrm {ID}_1(\mathcal A_2)]\to [\mathfrak M(\mathcal A),\mathbb S^2]$ , where $[\mathrm {ID}_1(\mathcal A_2)]$ is the set of connectivity components of the class of idempotent $2\times 2$ matrices with entries in $\mathcal A$ of constant rank  $1$ .

Proof In (a) and (c), the condition $\mathrm {dim}\,\mathfrak M(\mathcal A)\le 2$ is not required. In fact, the bijection $c_1$ is determined by assigning to a bundle its first Chern class, whereas the existence of the bijection i follows from the Novodvorskii–Taylor theory (see [23, Section 5.3, p. 186]). Finally, the existence of the bijection h under the condition $\mathrm {dim}\,\mathfrak M(\mathcal A)\le 2$ follows from the Hopf theorem (see, e.g., [16]).

Let us proceed to the proof of part (b) of the theorem.

Let $E\subset {\mathbb C}^n$ be a continuum with $\mathscr H^1(E)<\infty $ containing $\Gamma $ . Then, according to [13, Chapter 3, Exercise 3.5], there are functions $f_1,\dots , f_{n}\in \mathrm {Lip}(I)$ such that

$$\begin{align*}E\subset K:=(f_1,\dots, f_{n})(I)\quad \mathrm{and}\quad \mathscr H^1(K)\le 2\mathscr H^1(E). \end{align*}$$

By $A\subset \mathrm {Lip}(I)$ , we denote the closed unital subalgebra generated by $f_1,\dots , f_{n}$ . Since it is clear that $\mathrm {Lip}(I)$ is weakly inverse-closed, by Lemma 2.1, A is also weakly inverse-closed. Then the maximal ideal space of A is naturally identified with $\widehat K$ (see, e.g., [19, Proposition 1] and [14, Chapter III, Theorem 1.4]). Moreover, according to part (a) of the theorem, $\mathrm {dim}\,\widehat K\le 2$ .

We set $F:=(f_1,\dots , f_n): I\to {\mathbb C}^n$ . The algebra A is isomorphic to its Gelfand transform $\hat {A}$ —a complex Banach function algebra on $\widehat K=\mathfrak M(A)$ with a norm induced from A such that the pullback of $\hat A$ by F coincides with A (hence, ${\mathbb C} [z_1,\dots , z_n]|_{\widehat K}$ is a dense subalgebra of $\hat A$ ). Since $\mathfrak M(\hat A)=\widehat K$ as well, in the notation of Proposition 2.2, each

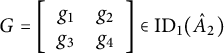(2.5) $$ \begin{align} G=\left[ \begin{array}{cc} g_1&g_2\\ g_3&g_4 \end{array} \right]\in \mathrm{ID}_1(\hat A_2) \end{align} $$

can be viewed as a map from $\widehat K$ to $M_2({\mathbb C})$ with coordinates in the algebra $\hat A$ whose image $\mathrm {ID}_1({\mathbb C}_2)$ consists of idempotent matrices of rank $1$ . Thus,

$$\begin{align*}Z=\left[ \begin{array}{cc} z_1&z_2\\ z_3&z_4 \end{array} \right] \in \mathrm{ID}_1({\mathbb C}_2) \end{align*}$$

if and only if $\mathrm {rank}\, Z=1$ and

$$\begin{align*}Z^2-Z=\left[ \begin{array}{ccc} z_1&z_2\\ z_3&z_4 \end{array} \right]\cdot \left[ \begin{array}{ccc} z_1-1&z_2\\ z_3&z_4-1 \end{array} \right]= \left[ \begin{array}{ccc} 0&0\\ 0&0 \end{array} \right], \end{align*}$$

which implies that

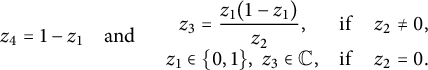(2.6) $$ \begin{align} z_4=1-z_1\quad \mathrm{and}\quad \begin{array}{ccc} \displaystyle z_3=\frac{z_1(1-z_1)}{z_2},&\mathrm{if}&z_2\ne 0,\\[4pt] z_1\in\{0,1\},\ z_3\in{\mathbb C},&\mathrm{if}&z_2=0. \end{array} \end{align} $$

Let $S:=G(K)=(G\circ F)(I)\subset M_2({\mathbb C})\cong {\mathbb C}^4$ . Since the entries of the map $G\circ F$ lie in $\mathrm {Lip}(I)$ , S is a continuum with $\mathscr H^1(S)<\infty $ . Moreover, $\hat A$ is contained in the uniform closure of ${\mathbb C} [z_1,\dots , z_n]|_{\widehat K}$ , which implies that $G(\widehat K)\subset \widehat S\subset \mathrm {ID}_1({\mathbb C}_2)$ . In addition, $\mathrm {dim}\,\widehat S\le 2$ by part (a) of the theorem. By the definition, the identity map ${\mathbb C}^4 \supset \mathrm {ID}_1({\mathbb C}_2)\to \mathrm {ID}_1({\mathbb C}_2)\subset M_2({\mathbb C})$ determines the holomorphic idempotent Z on $\mathrm {ID}_1({\mathbb C}_2)$ whose pullback by G coincides with $G\in \mathrm {ID}_1(\hat A_2)$ . According to Proposition 2.2, $Z|_{\widehat S}$ determines a complex rank-1 vector bundle over $\widehat S$ whose triviality implies that $Z|_{\widehat S}$ and, hence, G belong to the connectivity components (in $\mathrm {ID}_1(C(\widehat S)_2)$ and $\mathrm {ID}_1(\hat A_2)$ , respectively) of the constant idempotent $I_1\oplus 0_1$ . If the latter is true for all $G\in \mathrm {ID}_1(\hat A_2)$ , then Proposition 2.2 implies that $H^2(\widehat K,\mathbb {Z} )=0$ . However, $\widehat {\Gamma }\subset \widehat K$ and $\mathrm {dim}\,\widehat K\le 2$ and so the previous condition implies that $H^2(\widehat \Gamma ,\mathbb {Z} )=0$ by the Hopf theorem, as required. Thus, to complete the proof of the theorem, it suffices to prove the following lemma.

Lemma 2.3 Each complex rank-1 vector bundle over $\widehat S$ is trivial.

Proof Let V be a complex rank-1 vector bundle over $\widehat S$ . Consider the projection onto the first two coordinates $\pi : {\mathbb C}^4\to {\mathbb C}^2$ and $\pi (z_1,z_2,z_3, z_4):=(z_1,z_2)$ . For ${w_i=(i,0)}$ , $i=0,1$ , the sets $ \pi ^{-1}(w_i)\cap \mathrm {ID}_1({\mathbb C}_2)$ are biholomorphic to ${\mathbb C}$ (see (2.6)). Thus, $Z_i:=\pi ^{-1}(w_i)\cap \widehat S$ are homeomorphic to compact subsets of ${\mathbb C}$ ; hence, $H^2(Z_i,\mathbb {Z} )=0$ , $i=0,1$ . This implies that $V|_{Z_i}$ are trivial bundles. In particular, there are disjoint open neighborhoods $U_i\subset \widehat S$ of $Z_i$ and nonvanishing continuous sections $s_i:U_i\to V$ , ${i=0,1}$ . Since

$$\begin{align*}Z_i=\bigcap_{O_i\in \mathcal N(w_i)}\pi^{-1}(O_i)\cap\widehat S,\quad i=0,1, \end{align*}$$

where $\mathcal N(w_i)$ is the set of all open neighborhoods of $w_i$ , without loss of generality, we may assume that $U_i=\pi ^{-1}(O_i)\cap \widehat S$ for some $O_i\in \mathcal N(w_i)$ , $i=0,1$ . Let $U_2,\dots , U_k$ be relatively compact open subsets of $\widehat S\setminus \pi ^{-1}(w_i)$ such that $(U_i)_{i=0}^k$ is an open cover of $\widehat S$ and each $V|_{U_i}$ is trivial. Due to (2.6), $\pi $ maps $\widehat S\setminus (\pi ^{-1}(w_0)\cup \pi ^{-1}(w_1))$ homeomorphically onto $\pi (\widehat S)\setminus \{w_0,w_1\}$ . Thus, there exist (relatively compact) open subsets $O_i\subset \pi (\widehat S)\setminus \{w_0,w_1\}$ , $2\le i\le k$ , such that $\pi ^{-1}(O_i)\cap \widehat S=U_i$ . Let $s_i: U_i\to V$ be nonvanishing continuous sections of $V|_{U_i}$ , $i=2,\dots , k$ . Then V is determined by a continuous cocycle $\{c_{ij}\}_{0\le i,j\le k}$ ,

$$\begin{align*}c_{ij}:=s_i^{-1}\cdot s_j\in C(U_i\cap U_j,{\mathbb C}^*), \quad 0\le i,j\le k. \end{align*}$$

Furthermore, since each nonvoid $U_i\cap U_j$ is a subset of $\widehat S\setminus (\pi ^{-1}(w_0)\cup \pi ^{-1}(w_1))$ , due to (2.6), there exist $d_{ij}\in C(O_i\cap O_j,{\mathbb C}^*)$ such that $\pi ^{*}d_{ij}=c_{ij}$ . The family $\{d_{ij}\}_{0\le i,j\le k}$ is a $1$ cocycle on the cover $(O_i)_{0\le i\le k}$ of $\pi (\widehat S)$ , which determines a bundle $V'$ on $\widehat S$ such that $\pi ^*V'|_{\widehat S}=V$ . Thus, to complete the proof, it suffices to show that $V'$ is a trivial bundle.

Indeed, by definition, $\pi (\widehat S)\subset \widehat {\pi (S)}\subset {\mathbb C}^2$ . Since S is a continuum with ${\mathscr H^1(S)<\infty }$ , the set $\pi (S)=:(\pi \circ G\circ F)(I)$ is also a continuum with $\mathscr H^1(\pi (S))<\infty $ and so part (a) of the theorem implies that $\mathrm {dim}\, \widehat {\pi (S)}\le 2$ . In addition, $\widehat {\pi (S)}$ is a polynomially convex subset of ${\mathbb C}^2$ ; hence, $H^2(\widehat {\pi (S)},\mathbb {Z} )=0$ (see, e.g., [21, Corollary 2.3.6]). These imply that $H^2(\pi (\widehat S),\mathbb {Z} )=0$ by the Hopf theorem. In particular, each complex rank-1 vector bundle over $\pi (\widehat S)$ is trivial; hence, the bundle $V'$ is trivial as well, as required.

The proof of Theorem 1.6 is complete.

3 Proofs of Theorems 1.1, 1.2, and 1.4

Proof of Theorem 1.4

Let D be the set of all finite subsets of $A\cap BV(I)$ directed by inclusion $\subset $ . If $\alpha =\{f_{1,\alpha },\dots , f_{k_{\alpha },\alpha }\}\in D$ , we let $A_{\alpha }$ be the closed subalgebra of A generated by $\alpha $ . For $\alpha \subset \beta $ , we have $A_{\alpha }\subset A_{\beta }$ and we denote by $i_{\alpha }^{\beta }: A_{\alpha }\hookrightarrow A_{\beta }$ the corresponding inclusion map. Then $\{A_{\alpha }, i_{\alpha }^{\beta }\}$ is the injective system whose limit $A_*:=\varinjlim A_{\alpha }$ is a subalgebra of A containing $A\cap BV(I)$ . In particular, $ A_*$ is dense in A by the hypothesis, and hence the same is true for the images of $A_*$ and A in $C(\mathfrak M(A))$ under the Gelfand transform. Since by the hypothesis A is weakly inverse-closed, the latter along with Propositions 3 and 9 of [19] imply that the maximal ideal space $\mathfrak M(A)=\varprojlim \mathfrak M(A_{\alpha })$ —the projective limit of the adjoint projective system $\{\mathfrak M(A_{\alpha }), (i_{\alpha }^{\beta })^*\}$ of the maximal ideal spaces. Since $A_{\alpha }$ is generated by $f_{1,\alpha },\dots , f_{k_{\alpha },\alpha }\in BV(I)$ , the range of the map $F_{\alpha }=(f_{1,\alpha },\dots , f_{k_{\alpha },\alpha }): I\to {\mathbb C}^{k_{\alpha }}$ denoted by $\Gamma _{\alpha }$ is contained in a continuum with finite $\mathscr H^1$ measure (see, e.g., [13, Chapter 3, Exercise 3.1]). Moreover, by Lemma 2.1, $A_{\alpha }$ is weakly inverse-closed. Therefore, $\mathfrak M(A_{\alpha })$ is homeomorphic to $\widehat {\Gamma }_{\alpha }$ (see, e.g., [19, Proposition 1] and [14, Chapter III, Theorem 1.4]), and $\mathrm {dim}\,\widehat {\Gamma }_{\alpha }\le 2$ and $H^2(\widehat {\Gamma }_{\alpha },\mathbb {Z} )=0$ by Theorem 1.6. Then, since $\mathfrak M(A)=\varprojlim \mathfrak M(A_{\alpha })$ , $\mathrm {dim}\,\mathfrak M(A)\le 2$ (see, e.g., [12, Theorem 3.3.6]), and $H^2(\mathfrak M(A),\mathbb {Z} )=0$ (see, e.g., [11, Theorem 3.1, p. 261]), as required.

Proof of Theorem 1.1

Let M be a finitely generated projective A-module determined by an idempotent $I\in M_n(A)$ . The rank of M is a continuous $\mathbb {Z} _+$ -valued function on $\mathfrak M(A)$ equal to the rank of the Gelfand transform of I at points of $\mathfrak M(A)$ (see, e.g., [23, Section 7.6]). Let $0\le i_1<\cdots < i_k\le n$ be the range of this function, and let $\mathfrak M_s\subset \mathfrak M(A)$ be the clopen subset where $\hat {I}$ has constant rank $i_s$ . Then $\mathfrak M(A)=\sqcup _{s=1}^k\mathfrak M_s$ , and by the Shilov idempotent theory (see, e.g., [14, Chapter III, Corollary 6.5]), there exist idempotents $p_1,\dots , p_k\in A$ with $\sum _{s=1}^k p_s= 1_A$ such that the maximal ideal space of $A_{p_s}$ is $\mathfrak M_s$ . We have $A=\oplus _{s=1}^k A_{p_s}$ , which leads to the decomposition $I=\oplus _{s=1}^k\,p_s\cdot I$ , where $p_s\cdot I\in M_n(A_{p_s})$ is the idempotent determining the projective $A_{p_s}$ -module $M_{p_s}$ .

Next, due to the Novodvorskii–Taylor theory (see [23, Section 7.5, Theorem]), there exists a bijection between isomorphism classes of finitely generated projective $A_{p_s}$ -modules and complex vector bundles over $\mathfrak M_s$ . In our case, the isomorphism class of $M_{p_s}$ corresponds to the isomorphism class of a bundle $E_s$ over $\mathfrak M_s$ of complex rank $i_s$ . Since $\mathrm {dim}\, \mathfrak M_s\le 2$ and $H^2(\mathfrak M_s,\mathbb {Z} )=0$ by Theorem 1.4, the bundle $E_s$ is trivial (i.e., isomorphic to $\mathfrak M_s\times {\mathbb C}^{i_s}$ ), which implies that $M_{p_s}$ is isomorphic to the free module $(A_{p_s})^{i_s}$ , as required.

Proof of Theorem 1.2

Let $J\subset A\subset BV(I)$ be a closed ideal. Its hull $\mathcal Z( J)\subset \mathfrak M(A)$ is given by

$$\begin{align*}\mathcal Z(J):=\{x\in\mathfrak M(A)\,:\,\hat f(x)=0\quad\forall f\in J\}. \end{align*}$$

Consider the closed unital subalgebra $A_J:=\{c\cdot 1_A+f\,:\, c\in {\mathbb C},\ f\in J\}\subset A$ . By $Q_J: \mathfrak M(A)\rightarrow \mathfrak M(A_J)$ , we denote the continuous map transposed to the embedding $A_J\hookrightarrow A$ . Then $Q_J$ is a surjection which is one-to-one on $\mathfrak M(A)\setminus \mathcal Z(J)$ and sends $\mathcal Z(J)$ to a point (see, e.g., [3, Proposition 2.1] for the proof of a similar result). On the other hand, $A_J\subset BV(I)$ is weakly inverse-closed by Lemma 2.1, and so by Theorem 1.4, $\mathrm { dim}\,\mathfrak M(A_J)\le 2$ and $H^2(\mathfrak M(A_J),\mathbb {Z} )=0$ .

According to [22, Theorem 1.3], to prove that the stable rank of A is $1$ , it suffices to show that the relative Čech cohomology groups $H^2(\mathfrak M(A),\mathcal Z(J),\mathbb {Z} )=0$ for all ideals $J\subset A$ . However, due to the strong excision property for cohomology (see, e.g., [20, Chapter 6, Theorem 5]), the pullback map $Q_J^*$ induces an isomorphism of the Čech cohomology groups $H^2(\mathfrak M(A_J),\mathbb {Z} )\cong H^2(\mathfrak M(A),\mathcal Z(J),\,\mathbb {Z} )$ . In particular, $H^2(\mathfrak M(A),\mathcal Z(J),\,\mathbb {Z} )=0$ , as required.

4 Concluding remarks

There are some applications of Theorems 1.1 and 1.2 to operator-valued $BV(I)$ functions and to interpolating problems for $BV(I)$ maps into some complex manifolds analogous to those of [4, Section 1.2] and [5, Theorems 1.4, 1.6]. These results will be published elsewhere. Here, we formulate one of such results.

Let $A\subset BV(I)$ be a weakly inverse-closed complex Banach function algebra, and let $L(X)$ be the Banach algebra of bounded linear operators on a complex Banach space X equipped with the operator norm. Let $\alpha $ be either the projective cross norm $\pi $ or the injective cross norm $\varepsilon $ on the algebraic tensor product $A\otimes L(X)$ , and let $A\widehat {\otimes }_{\alpha } L(X)$ be the completion with respect to $\alpha $ . If $\alpha =\varepsilon $ , we additionally assume that the algebra A is uniform (i.e., $\|a^2\|=\|a\|^2$ for all $a\in A$ ). Then $A\widehat {\otimes }_{\alpha } L(X)$ is also a Banach algebra (see, e.g., [10, Section 1.3] for the references). We denote by $(A\widehat {\otimes }_{\alpha } L(X))^{-1}$ and $\mathrm {id}\, A\widehat {\otimes }_{\alpha } L(X)=\{F\in A\widehat {\otimes }_{\alpha } L(X)\, :\, F^2=F\}$ the group of invertible elements and the set of idempotents of $A\widehat {\otimes }_{\alpha } L(X)$ .

We say that idempotents $F_1,F_2\in \mathrm {id}\, A\widehat {\otimes }_{\alpha } L(X)$ are equivalent if $F_2=G^{-1}\cdot F_1\cdot G$ for some $G\in (A\widehat {\otimes }_{\alpha } L(X))^{-1}$ .

An idempotent $F\in \mathrm {id}\, A\widehat {\otimes }_{\alpha } L(X)$ is said to be locally constant if there exist idempotents $p_1,\dots , p_k\in A$ with $\sum _{j=1}^k p_j=1_I$ and $I_1,\dots , I_k\in L(X)$ , $k\in \mathbb {N}$ , such that

$$\begin{align*}F=\sum_{j=1}^k p_j\otimes I_j. \end{align*}$$

With the above notation, we have the following generalization of Theorem 1.1.

Theorem Suppose that X is isomorphic to one of the spaces: a Hilbert space, $c_0$ , or $\ell ^p$ , $1\le p\le \infty $ . Then every idempotent in $\mathrm {id}\, A\widehat {\otimes }_{\alpha } L(X)$ is equivalent to a locally constant idempotent.