Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T15:03:45.920Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantum Deformations of Simple Lie Algebras

Published online by Cambridge University Press:  20 November 2018

Murray Bremner
Murray Bremner*
Affiliation:
Department of Mathematics and Statistics University of Saskatchewan Room 142 McLean Hall 106 Wiggins Road Saskatoon, SK S7N 5E6, e-mail: bremner@math.usask.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is shown that every simple complex Lie algebra 𝔤 admits a 1-parameter family 𝔤q of deformations outside the category of Lie algebras. These deformations are derived from a tensor product decomposition for Uq(𝔤)-modules; here Uq(𝔤) is the quantized enveloping algebra of 𝔤. From this it follows that the multiplication on 𝔤q is Uq(𝔤)-invariant. In the special case 𝔤 = 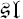(2), the structure constants for the deformation 𝔤 (2)q are obtained from the quantum Clebsch-Gordan formula applied to V(2)q ⊗ V(2)q; here V(2)q is the simple 3-dimensional Uq(𝔤(2))-module of highest weight q2.

Keywords

Primary: 17B37Secondary: 17A01
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 40 , Issue 2 , 01 June 1997 , pp. 143 - 148
Copyright
Copyright © Canadian Mathematical Society 1997

References

[CP] Chari, V. and Pressley, A., A Guide to Quantum Groups, Cambridge, 1994.Google Scholar
[DH] Delius, G. W. and A. Ḧuffmann, On quantum Lie algebras and quantum root systems, MSRI preprints on quantum algebra and topology, q-alg/9506017.Google Scholar
[DHGZ] Delius, G. W., A. Ḧuffmann, Gould, M. D. and Zhang, Y.-Z., Quantum Lie algebras associated to Uq( n) and Uq( n), MSRI preprints on quantum algebra and topology, q-alg/9508013.Google Scholar
[J] Jantzen, J. C., Lectures on Quantum Groups, American Mathematical Society, 1995.Google Scholar
[K] Kassel, C., Quantum Groups, Springer-Verlag, 1995.Google Scholar
[Li] Liu, K.-Q., Characterizations of the quantum Witt algebra, Lett. Math. Phys. 24 (1992), 257–265.Google Scholar
[Lu] Lusztig, G., Introduction to Quantum Groups, Birkhäuser, 1993.Google Scholar
[LS] Lyubashenko, V. and Sudbery, A., Quantum Lie algebras of type An, MSRI preprints on quantum algebra and topology, q-alg/9510004.Google Scholar