Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-11T00:46:56.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantum Ergodicity of Boundary Values of Eigenfunctions: A Control Theory Approach

Published online by Cambridge University Press:  20 November 2018

N. Burq
N. Burq*
Affiliation:
Université Paris Sud Mathématiques, Bât 425, 91405 Orsay Cedex, France e-mail: Nicolas.burq@math.u-psud.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

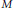Consider $M$, a bounded domain in 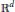${{\mathbb{R}}^{d}}$, which is a Riemanian manifold with piecewise smooth boundary and suppose that the billiard associated to the geodesic flow reflecting on the boundary according to the laws of geometric optics is ergodic. We prove that the boundary value of the eigen-functions of the Laplace operator with reasonable boundary conditions are asymptotically equidistributed in the boundary, extending previous results by Gérard and Leichtnam as well as Hassell and Zelditch, obtained under the additional assumption of the convexity of 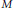$M$.

Résumé

Résumé

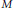Soit $M$ un domain borné de 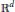${{\mathbb{R}}^{d}}$ qui est une variété riemanienne à coins. On suppose que le billard défini par le flot géodésique brisé est ergodique. On démontre que les valeurs au bord des fonctions propres du Laplacien (avec des conditions aux limites raisonnables) sont asymptotiquement équidistribuées dans le bord. Ceci généralise des résultats antérieurs, de P. Gérard et E. Leichtnamaussi bien que A. Hassell et S. Zelditch, obtenus sous l’hypothèse supplémentaire de convexité géodésique du domaine.

Keywords

35Q5535BXX37K0537L5081Q20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 1 , 01 March 2005 , pp. 3 - 15
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Bardos, C., Lebeau, G., and Rauch, J., Sharp sufficient conditions for the observation, control and stabilization of waves from the boundary. Siam J. Control Optim. 305(1992), 1024–1065.Google Scholar
[2] Burq, N. and Gérard, P., Condition nécessaire et suffisante pour la contrôlabilité exacte des ondes. C. R. Acad. Sci. Paris Sér. I Math. 325(1997), 749–752.Google Scholar
[3] Burq, N. and Lebeau, G.. Mesures de défaut de compacité, application au système de Lamé. Ann. Sci. École Norm. Sup. 34(2001), 817–870.Google Scholar
[4] Burq, N.. Mesures semi-classiques et mesures de défaut. Astérisque 245(1997) 167–195.Google Scholar
[5] Chazarain, Jacques and Piriou, Alain. Introduction to the theory of linear partial differential equations. Studies in Mathematics and its Applications, 14, North-Holland, Amsterdam, 1982.Google Scholar
[6] de Verdière, Y. Colin. Ergodicité et fonctions propres du laplacien. Comm. Math. Phys. 102(1985), 187–214.Google Scholar
[7] Gérard, P. and Leichtnam, E.. Ergodic properties of eigenfunctions for the Dirichlet problem. Duke Math. J. 71(1993), 559–607.Google Scholar
[8] Hassell, A. and Zelditch, S.. Quantum ergodicity of boundary values of eigenfunctions. Preprint, 2002.Google Scholar
[9] Lions, P. L. and Paul, T.. Sur les mesures de Wigner. Rev.Mat. Iberoamerican. 9(1993), 553–618.Google Scholar
[10] Shnirelman, A. I.. Ergodic properties of eigenfunctions. Uspekhi Mat. Nauk. 29(1974), 181–182.Google Scholar
[11] Zelditch, S.. Uniform distribution of eigenfunctions on compact hyperbolic surfaces. Duke Math. J. 55(1987), 919–941.Google Scholar
[12] Zelditch, S. and Zworski, M.. Ergodicity of eigenfunctions for ergodic billiards. Comm. Math. Phy. 175(1996), 673–682.Google Scholar