Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T08:10:57.725Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasiconvexity and Density Topology

Published online by Cambridge University Press:  20 November 2018

Patrick J. Rabier
Patrick J. Rabier*
Affiliation:
Department of Mathematics, University of Pittsburgh, Pittsburgh, PA 15260, USA e-mail: rabier@imap.pitt.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that if 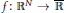$f\,:\,{{\mathbb{R}}^{N}}\,\to \,\overline{\mathbb{R}}$ is quasiconvex and 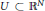$U\,\subset \,{{\mathbb{R}}^{N}}$ is open in the density topology, then 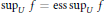$\underset{U}{\mathop{\sup }}\,f=\text{ess}\,\underset{U}{\mathop{\sup }}\,f$, while 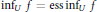${{\inf }_{U}}\,f\,=\,\text{ess}\,{{\inf }_{U}}\,f$ if and only if the equality holds when 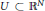$U\,\subset \,{{\mathbb{R}}^{N}}$. The first (second) property is typical of 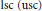$\text{lsc}\,\text{(usc)}$ functions, and, even when 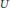$U$ is an ordinary open subset, there seems to be no record that they both hold for all quasiconvex functions.

This property ensures that the pointwise extrema of 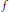$f$ on any nonempty density open subset can be arbitrarily closely approximated by values of 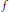$f$ achieved on “large” subsets, which may be of relevance in a variety of situations. To support this claim, we use it to characterize the common points of continuity, or approximate continuity, of two quasiconvex functions that coincide away from a set of measure zero.

Keywords

52A4126B05density topologyquasiconvex functionapproximate continuitypoint of continuity
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 1 , 14 March 2014 , pp. 178 - 187
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Borwein, J. M. and Wang, X., Cone-monotone functions: differentiability and continuity. Canad. J. Math. 57 (2005), no. 5, 961–982. http://dx.doi.org/10.4153/CJM-2005-037-5 Google Scholar
[2] Chabrillac, Y. and Crouzeix, J.-P., Continuity and differentiability properties of monotone realfunctions of several variables. Nonlinear analysis and optimization (Louvain-la-Neuve, 1983). Math. Programming Stud. 30 (1987), 1–16.Google Scholar
[3] Crouzeix, J.-P., Some differentiability properties of quasiconvex functions on Rn. In: Optimization and optimal control (Proc. Conf. Math. Res. Inst., Oberwolfach, 1980), Lecture Notes in Control and Information Sciences, 30, Springer, Berlin-New York, 1981, pp. 9–20.Google Scholar
[4] Fenchel, W. and Blackett, D.W., Convex cones, sets and functions. Princeton University, Department of Mathematics, Princeton, 1953.Google Scholar
[5] de Finetti, B., Sulle stratificazioni convesse. Ann. Mat. Pura Appl. 30 (1949), 173–183. http://dx.doi.org/10.1007/BF02415006 Google Scholar
[6] Goffman, C., Neugebauer, C. J., and Nishiura, T., Density topology and approximate continuity. Duke Math. J. 28 (1961), 497–505. http://dx.doi.org/10.1215/S0012-7094-61-02847-2 Google Scholar
[7] Guerraggio, A. and Molho, E., The origins of quasi-concavity: a development between mathematicsand economics. Historia Math. 31 (2004), no. 1, 62–75. http://dx.doi.org/10.1016/j.hm.2003.07.001 Google Scholar
[8] Haupt, O. and Pauc, C., La topologie approximative de Denjoy envisagée comme vraie topologie. C. R. Acad. Sci. Paris 234 (1952), 390–392.Google Scholar
[9] Hiriart-Urruty, J.-B. and Lemaréchal, C., Convex analysis and minimization algorithms. I.Fundamentals, Grundlehren der MathematischenWissenschaften, 305, Springer-Verlag, Berlin 1993.Google Scholar
[10] Jones, F., Lebesgue integration on euclidean space. Jones and Bartlett, Boston, MA, 1993.Google Scholar
[11] Lukeš, J., Malý, J., and Zajĭček, L., Fine topology methods in real analysis and potential theory. Lecture Notes in Mathematics, 1189, Springer-Verlag, Berlin, 1986.Google Scholar
[12] Martin, N. F. G., A topology for certain measure spaces. Trans. Amer. Math. Soc. 112 (1964), 1–18. http://dx.doi.org/10.1090/S0002-9947-1964-0161953-5 Google Scholar
[13] Rabier, P. J., Points of continuity of quasiconvex functions on topological vector spaces. arxiv:1206.5775.Google Scholar
[14] Rockafellar, R. T., Convex analysis. Princeton Mathematical Series, 28, Princeton University Press, Princeton, NJ, 1970.Google Scholar
[15] Troyer, R. J. andZiemer, W. P., Topologies generated by outer measures. J. Math. Mech. 12 (1963), 485–494.Google Scholar