Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T14:43:07.879Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-copure Submodules

Published online by Cambridge University Press:  20 November 2018

Saeed Rajaee
Saeed Rajaee*
Affiliation:
Department of Mathematics, Faculty of Mathematics, Payame Noor University (PNU), P.O. Box, 19395-3697, Tehran, Iran e-mail: saeed_rajaee@pnu.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

All rings are commutative with identity, and all modules are unital. In this paper we introduce the concept of a quasi-copure submodule of a multiplication $R$-module 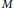$M$ and will give some results about it. We give some properties of the tensor product of finitely generated faithful multiplication modules.

Keywords

13A1513C0513C1313C99multiplication modulearithmetical ringcopure submoduleradical of submodules
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 1 , 01 March 2016 , pp. 197 - 203
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Ali, M. M., 1/2 cancellation modules and homogeneous idealization. IL Comm. Algebra 36(2008), 3842–3864. http://dx.doi.Org/10.1080/00927870802160826 Google Scholar
[2] Ali, M. M., Multiplication modules and tensor product. Beitrâge Algebra Geom. 47(2006), no. 2, 305–327.Google Scholar
[3] Ali, M. M., Some remarks on Multiplication and flat modules. J. Commut. Algebra 4(2012), no. 1, 1–27. http://dx.doi.Org/10.121 6/JCA-2O12-4-1-1 Google Scholar
[4] Ali, M. M., Some remarks on multiplication and projective modules. IL Comm. Algebra 41(2013), 195–214. http://dx.doi.Org/10.1080/00927872.2011.628724 Google Scholar
[5] Ansari-Toroghy, H. and Farshadifar, F.. On comultiplication modules. Korean Ann Math. 25(2008), no. 1-2, 57–66.Google Scholar
[6] Barnard, A. D., Multiplication modules. J. Algebra 71(1981), 174–178. http://dx.doi.Org/10.101 6/0021-8693(81)90112-5 Google Scholar
[7] El-Bast, Z. A. and Smith, P. F., Multiplication modules. Comm. Algebra 16(1988), 755–779. http://dx.doi.Org/10.1080/00927878808823601 Google Scholar
[8] Faith, C., Algebra I: Rings, modules, and categories. Grundlehren der Mathematischen Wissenschaften, 190, Springer-Verlag, Berlin-New York, 1981.Google Scholar
[9] McCasland, R. L. and Moore, M. E., On radicals of finitely generated modules. Canad. Math. Bull. 29(1986), no. 1, 37–39. http://dx.doi.Org/10.4153/CMB-1986-006-7 Google Scholar
[10] Naoum, A. G. and Al-Alwan, F. H., Dedekind modules. Comm. Algebra 24(1996), no. 2. 397–412. http://dx.doi.Org/10.1080/00927879608825576 Google Scholar
[11] Smith, P. F., Some remarks on multiplication modules. Arch. Math. (Basel) 50(1988), 223–235. http://dx.doi.Org/10.1007/BF01187738 Google Scholar