Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T17:43:02.712Z Has data issue: false hasContentIssue false
  • English
  • Français

The Range of the Cesàro Operator Acting on 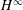$H^{\infty }$

Part of: Spaces and algebras of analytic functions Special classes of linear operators Other generalizations

Published online by Cambridge University Press:  04 December 2019

Guanlong Bao ,
Hasi Wulan  and
Fangqin Ye
Guanlong Bao
Affiliation:
Department of Mathematics, Shantou University, Shantou515063, Guangdong, China Email: glbao@stu.edu.cnwulan@stu.edu.cn
Hasi Wulan
Affiliation:
Department of Mathematics, Shantou University, Shantou515063, Guangdong, China Email: glbao@stu.edu.cnwulan@stu.edu.cn
Fangqin Ye
Affiliation:
Business School, Shantou University, Shantou515063, Guangdong, China Email: fqye@stu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1993, N. Danikas and A. G. Siskakis showed that the Cesàro operator 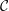${\mathcal{C}}$ is not bounded on 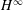$H^{\infty }$; that is, 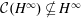${\mathcal{C}}(H^{\infty })\nsubseteq H^{\infty }$, but 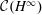${\mathcal{C}}(H^{\infty })$ is a subset of 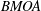$BMOA$. In 1997, M. Essén and J. Xiao gave that 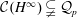${\mathcal{C}}(H^{\infty })\subsetneq {\mathcal{Q}}_{p}$ for every 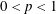$0<p<1$. In this paper, we characterize positive Borel measures 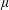$\unicode[STIX]{x1D707}$ such that 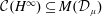${\mathcal{C}}(H^{\infty })\subseteq M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$ and show that 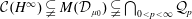${\mathcal{C}}(H^{\infty })\subsetneq M({\mathcal{D}}_{\unicode[STIX]{x1D707}_{0}})\subsetneq \bigcap _{0<p<\infty }{\mathcal{Q}}_{p}$ by constructing some measures 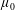$\unicode[STIX]{x1D707}_{0}$. Here, 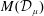$M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$ denotes the Möbius invariant function space generated by 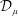${\mathcal{D}}_{\unicode[STIX]{x1D707}}$, where 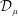${\mathcal{D}}_{\unicode[STIX]{x1D707}}$ is a Dirichlet space with superharmonic weight induced by a positive Borel measure 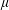$\unicode[STIX]{x1D707}$ on the open unit disk. Our conclusions improve results mentioned above.

Keywords

The Cesàro operatorH∞Möbius invariant function spacesuperharmonic function

MSC classification

Primary: 47B38: Operators on function spaces (general)
Secondary: 30H25: Besov spaces and $Q_p$-spaces 31C25: Dirichlet spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 3 , September 2020 , pp. 633 - 642
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work was supported by NNSF of China (No. 11801347, No. 11720101003 and No. 11571217), NSF of Guangdong Province (No. 2018A030313512), Department of Education of Guangdong Province (No. 2017KQNCX078), Key projects of fundamental research in universities of Guangdong Province (No. 2018KZDXM034), and STU SRFT (No. NTF17020 and No. STF17005). F. Ye is the corresponding author.

References

Aleman, A., Hilbert spaces of analytic functions between the Hardy and the Dirichlet space. Proc. Amer. Math. Soc. 115(1992), 97–104. https://doi.org/10.2307/2159570CrossRefGoogle Scholar
Aleman, A., The Multiplication Operator on Hilbert Spaces of Analytic Functions. Habilitation, FernUniversität Hagen, 1993.Google Scholar
Aulaskari, R., Xiao, J., and Zhao, R., On subspaces and subsets of BMOA and UBC. Analysis 15(1995), 101–121. https://doi.org/10.1524/anly.1995.15.2.101CrossRefGoogle Scholar
Baernstein, A., Analytic functions of bounded mean oscillation. In: Aspects of contemporary complex analysis (Proc. NATO Adv. Study Inst., Univ. Durham, Durham, 1979). Academic Press, London–New York, 1980, pp. 3–36.Google Scholar
Bao, G., Göğüş, N. G., and Pouliasis, S., On Dirichlet spaces with a class of superharmonic weights. Canad. J. Math. 70(2018), 721–741. https://doi.org/10.4153/CJM-2017-005-1CrossRefGoogle Scholar
Bao, G., Göğüş, N. G., and Pouliasis, S., Intersection of harmonically weighted Dirichlet spaces. C. R. Math. Acad. Sci. Paris 355(2017), 859–865. https://doi.org/10.1016/j.crma.2017.07.013CrossRefGoogle Scholar
Bao, G., Göğüş, N. G., and Pouliasis, S., 𝓠p spaces and Dirichlet type spaces. Canad. Math. Bull. 60(2017), 690–704. https://doi.org/10.4153/CMB-2017-006-1CrossRefGoogle Scholar
Bao, G., Mashreghi, J., Pouliasis, S., and Wulan, H., Möbius invariant function spaces and Dirichlet spaces with superharmonic weights. J. Aust. Math. Soc. 106(2019), 1–18. https://doi.org/10.1017/S1446788718000022CrossRefGoogle Scholar
Cowen, C. C., Subnormality of the Cesáro operator and a semigroup of composition operators. Indiana Univ. Math. J. 33(1984), 305–318. https://doi.org/10.1512/iumj.1984.33.33017CrossRefGoogle Scholar
Danikas, N. and Siskakis, A. G., The Cesàro operator on bounded analytic functions. Analysis 13(1993), 295–299. https://doi.org/10.1524/anly.1993.13.3.295CrossRefGoogle Scholar
Duren, P., Theory of H p spaces. Academic Press, New York, 1970.Google Scholar
El-Fallah, O., Kellay, K., Klaja, H., Mashreghi, J., and Ransford, T., Dirichlet spaces with superharmonic weights and de Branges–Rovnyak spaces. Complex Anal. Oper. Theory 10(2016), 97–107. https://doi.org/10.1007/s11785-015-0474-7CrossRefGoogle Scholar
Essén, M. and Wulan, H., On analytic and meromorphic function and spaces of 𝓠K-type. Illinois J. Math. 46(2002), 1233–1258.CrossRefGoogle Scholar
Essén, M. and Xiao, J., Some results on 𝓠p spaces, 0 < p < 1. J. Reine Angew. Math. 485(1997), 173–195.Google Scholar
Girela, D., Analytic functions of bounded mean oscillation. In: Complex Function Spaces (Mekrijärvi, 1999). Univ. Joensuu Dept. Math. Rep. Ser. 4, Univ. Joensuu, Joensuu, 2001, pp. 61–170.Google Scholar
Hedenmalm, H., Korenblum, B., and Zhu, K., Theory of Bergman spaces. Springer-Verlag, New York, 2000. https://doi.org/10.1007/978-1-4612-0497-8CrossRefGoogle Scholar
John, F. and Nirenberg, L., On functions of bounded mean oscillation. Comm. Pure Appl. Math. 14(1961), 415–426. https://doi.org/10.1002/cpa.3160140317CrossRefGoogle Scholar
Kriete, T. L. and Trutt, D., The Cesáro operator in ℓ 2 is subnormal. Amer. J. Math. 93(1971), 215–225. https://doi.org/10.2307/2373458CrossRefGoogle Scholar
Miao, J., The Cesáro operator is bounded on H p for 0 < p < 1. Proc. Amer. Math. Soc. 116(1992), 1077–1079. https://doi.org/10.2307/2159491Google Scholar
Richter, S., A representation theorem for cyclic analytic two-isometries. Trans. Amer. Math. Soc. 328(1991), 325–349. https://doi.org/10.2307/2001885CrossRefGoogle Scholar
Siskakis, A. G., Composition semigroups and the Cesáro operator on H p. J. London Math. Soc. 36(1987), 153–164. https://doi.org/10.1112/jlms/s2-36.1.153CrossRefGoogle Scholar
Siskakis, A. G., The Cesáro operator is bounded on H 1. Proc. Amer. Math. Soc. 110(1990), 461–462. https://doi.org/10.2307/2048089Google Scholar
Wulan, H. and Zhu, K., Möbius invariant 𝓠K spaces. Springer, Cham, 2017. https://doi.org/10.1007/978-3-319-58287-0CrossRefGoogle Scholar
Xiao, J., Holomorphic 𝓠 classes. Lecture Notes in Mathematics, 1767, Springer-Verlag, Berlin, 2001. https://doi.org/10.1007/b87877CrossRefGoogle Scholar
Xiao, J., Geometric 𝓠p Functions. Birkhäuser Verlag, Basel–Boston–Berlin, 2006.Google Scholar
Xiao, J., The 𝓠p corona theorem. Pacific J. Math. 194(2000), 491–509. https://doi.org/10.2140/pjm.2000.194.491CrossRefGoogle Scholar
Zhu, K., Operator theory in function spaces, Second ed., Mathematical Surveys and Monographs, 138, American Mathematical Society, Providence, RI, 2007. https://doi.org/10.1090/surv/138CrossRefGoogle Scholar