Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T14:31:29.884Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational Points in Arithmetic Progressions on y2 = xn + k

Published online by Cambridge University Press:  20 November 2018

Maciej Ulas
Maciej Ulas*
Affiliation:
Jagiellonian University, Institute of Mathematics, 30 - 348 Kraków, Poland e-mail: maciej.ulas@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 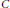$C$ be a hyperelliptic curve given by the equation 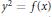${{y}^{2}}\,=\,f(x)$ for 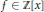$f\,\in \,\mathbb{Z}[x]$ without multiple roots. We say that points 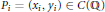${{P}_{i}}\,=\,({{x}_{i}},\,{{y}_{i}})\,\in \,C(\mathbb{Q})$ for 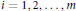$i\,=\,1,\,2,\,\ldots ,\,m$ are in arithmetic progression if the numbers ${{x}_{i}}$ for 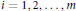$i\,=\,1,\,2,\,\ldots ,\,m$ are in arithmetic progression.

In this paper we show that there exists a polynomial 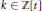$k\,\in \,\mathbb{Z}[t]$ with the property that on the elliptic curve 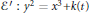$\varepsilon \prime :{{y}^{2}}={{x}^{3}}+k(t)$ (defined over the field 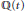$\mathbb{Q}(t)$) we can find four points in arithmetic progression that are independent in the group of all 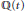$\mathbb{Q}(t)$-rational points on the curve 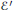$\varepsilon \prime $. In particular this result generalizes earlier results of Lee and Vélez. We also show that if 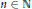$n\,\in \,\mathbb{N}$ is odd, then there are infinitely many $k$'s with the property that on curves ${{y}^{2}}\,=\,{{x}^{n}}\,+\,k$ there are four rational points in arithmetic progressions. In the case when $n$ is even we can find infinitely many $k$'s such that on curves ${{y}^{2}}\,=\,{{x}^{n}}\,+\,k$ there are six rational points in arithmetic progression.

Keywords

11G05arithmetic progressionselliptic curvesrational points on hyperelliptic curves
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 1 , 01 March 2012 , pp. 193 - 207
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Bremner, A., On the equation Y 2 = X 5 + k. Experiment. Math. 17(2008), no. 3, 371–374.Google Scholar
[2] Connell, I., APECS: Arithmetic of plane elliptic curves, 2001. http://www.math.mcgill.ca/connell/public/apecs.Google Scholar
[3] Elkies, N. D., On A 4 + B 4 + C 4 = D 4 . Math. Comp. 51(1988), no. 184, 825–835.Google Scholar
[4] Faltings, G., Endlichkeitssätze für abelsche Varietäten über Zahlkörpern. Invent. Math. 73(1983), no. 3, 349–366. doi:10.1007/BF01388432Google Scholar
[5] Lee, J.-B. and Vélez, W. Y., Integral solutions in arithmetic progression for y 2 = x 3 + k. Period. Math. Hungar. 25(1992), no. 1, 31–49. doi:10.1007/BF02454382Google Scholar
[6] Mohanty, S. P., Integral solutions in arithmetic progression for y 2 = x 3 + k. Acta Math. Acad. Sci. Hungar. 34(1980), no. 3–4, 261–265. doi:10.1007/BF01898141Google Scholar
[7] Mordell, L. J., Diophantine equations. Pure and Applied Mathematics, 30, Academic Press, London-New York, 1969.Google Scholar
[8] Shioda, T., On elliptic modular surfaces. J. Math. Soc. Japan 24(1972), 20–59. doi:10.2969/jmsj/02410020Google Scholar
[9] Silverman, J. H., The arithmetic of elliptic curves. Graduate Texts in Mathematics, 106, Springer-Verlag, New York, 1986.Google Scholar
[10] Skolem, T., Diophantische Gleichungen. Ergebnisse der Mathematik und ihrer Grenzgebiete, 5, no. 4, Berlin, Springer, 1938.Google Scholar