Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T06:23:34.311Z Has data issue: false hasContentIssue false
  • English
  • Français

Real-Analytic Negligibility of Points and Subspaces in Banach Spaces, with Applications

Published online by Cambridge University Press:  20 November 2018

D. Azagra  and
T. Dobrowolski
D. Azagra
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias Matemáticas, Universidad Complutense, Madrid 28040, Spain, email: daniel@sunam1.mat.ucm.es
T. Dobrowolski
Affiliation:
Department of Mathematics, Pittsburg State University, Pittsburg, Kansas 66762, USA, email: tdobrowo@mail.pittstate.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that every infinite-dimensional Banach space 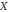$X$ having a (not necessarily equivalent) real-analytic norm is real-analytic diffeomorphic to $X\,\backslash \,\left\{ 0 \right\}$. More generally, if 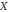$X$ is an infinite dimensional Banach space and 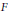$F$ is a closed subspace of 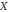$X$ such that there is a real-analytic seminorm on 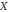$X$ whose set of zeros is 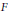$F$, and 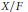$X/F$ is infinite-dimensional, then 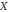$X$ and $X\backslash F$ are real-analytic diffeomorphic. As an application we show the existence of real-analytic free actions of the circle and the $n$-torus on certain Banach spaces.

Keywords

46B2058B99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 1 , 01 March 2002 , pp. 3 - 10
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Azagra, D., Smooth negligibility and sub differential calculus in Banach spaces, with applications. Doctoral dissertation, Universidad Complutense de Madrid, December 1997.Google Scholar
[2] Azagra, D., Diffeomorphisms between spheres and hyperplanes in infinite-dimensional Banach spaces. Studia Math. (2) 125 (1997), 179–186.Google Scholar
[3] Azagra, D. and Dobrowolski, T., Smooth negligibility of compact sets in infinite-dimensional Banach spaces, with applications. Math. Ann. (3) 312 (1998), 445–463.Google Scholar
[4] Azagra, D., Gómez, J., and Jaramillo, J. A., Rolle's theorem and negligibility of points in infinite-dimensional Banach spaces. J. Math. Anal. Appl. (2) 213 (1997), 487–495.Google Scholar
[5] Bessaga, C., Every infinite-dimensional Hilbert space is diffeomorphic with its unit sphere. Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 14 (1966), 27–31.Google Scholar
[6] Bessaga, C., Negligible sets in linear topological spaces. Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 16 (1968), 117–119.Google Scholar
[7] Bessaga, C., Interplay Between Infinite-Dimensional Topology and Functional Analysis. Mappings Defined by Explicit Formulas and Their Applications. Topology Proc. 19 (1994), 15–35.Google Scholar
[8] Bessaga, C. and Klee, V. L., Two topological properties of topological linear spaces. Israel J. Math. 2 (1964), 211–220.Google Scholar
[9] Bessaga, C. and Klee, V. L., Every non-normable Fréchet space is homeomorphic with all of its closed convex bodies. Math. Ann. 163 (1966), 161–166.Google Scholar
[10] Bessaga, C. and Pełczyński, A., Selected topics in infinite-dimensional topology. Monografie Matematyczne 58, Polish Scientific Publishers, Warsaw, 1975.Google Scholar
[11] Burghelea, D. and Kuiper, N. H., Hilbert manifolds. Ann. of Math. 90 (1969), 379–417.Google Scholar
[12] Corson, H. H. and Klee, V. L., Topological classification of convex sets. Proc. Symp. Pure Math. 7, Amer.Math. Soc., Providence, RI, 1963, 37–51.Google Scholar
[13] Deville, R., Godefroy, G., and Zizler, V., Smoothness and renormings in Banach spaces. Pitman Monographies and Surveys in Pure and Applied Mathematics 64, 1993.Google Scholar
[14] Diestel, J., Geometry of Banach Spaces—Selected Topics. Lecture Notes in Math. 485, Springer-Verlag, New York, 1975.Google Scholar
[15] Dieudonné, J., Foundations of Modern Analysis. Academic Press, New York-London, 1960.Google Scholar
[16] Dobrowolski, T., Smooth and R-analytic negligibility of subsets and extension of homeomorphism in Banach spaces. Studia Math. 65 (1979), 115–139.Google Scholar
[17] Dobrowolski, T., Every Infinite-Dimensional Hilbert Space is Real-Analytically Isomorphic with Its Unit Sphere. J. Funct. Anal. 134 (1995), 350–362.Google Scholar
[18] Dobrowolski, T., Relative Classification of Smooth Convex Bodies. Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 25 (1977), 309–312.Google Scholar
[19] Garay, B. M., Cross sections of solution funnels in Banach spaces. StudiaMath. 97 (1990), 13–26.Google Scholar
[20] Garay, B. M., Deleting Homeomorphisms and the Failure of Peano's Existence Theorem in Infinite-Dimensional Banach Spaces. Funkcialaj Ekvacioj 34 (1991), 85–93.Google Scholar
[21] Garay, B. M., Parallelizability in Banach spaces I-II-III, Acta Math. Hungar., Proc Roy. Soc. Edinburgh, Proc. Banach Center Sem.Google Scholar
[22] Goebel, K. and Wósko, J., Making a hole in the space. Proc. Amer. Math. Soc. 114 (1992), 475–476.Google Scholar
[23] James, R. C., Weakly compact sets. Trans. Amer.Math. Soc. 113 (1964), 129–140.Google Scholar
[24] John, K., Toruńczyck, H. and Zizler, V., Uniformly smooth partitions of unity on superreflexive spaces. Studia Math. 70 (1981), 129–137.Google Scholar
[25] Klee, V. L., Convex bodies and periodic homeomorphisms in Hilbert space. Trans. Amer.Math. Soc. 74 (1953), 10–43.Google Scholar
[26] Smith, P. A., Fixed-point theorems for periodic transformations. Amer. J.Math. 63 (1941), 1–8.Google Scholar
[27] Stoker, J. J., Unbounded convex point sets. Amer. J.Math. 62 (1940), 165–179.Google Scholar
[28] Whittlesey, E. F., Analytic functions in Banach spaces. Proc. Amer.Math. Soc. 16 (1965), 1077–1083.Google Scholar