Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-18T18:22:13.194Z Has data issue: false hasContentIssue false
  • English
  • Français

Reflexive Homomorphic Relations

Published online by Cambridge University Press:  20 November 2018

G. D. Findlay
G. D. Findlay*
Affiliation:
McGill University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that a symmetric and transitive relation on a set is reflexive wherever it is defined. In this note we show that a converse is true for homomorphic relations in certain classes of algebras.

Consider a class 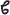of similar algebras which contains the sub-algebras and quotient algebras of each of its members. Assume also that the direct product A x B of each pair A, B in 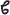is also an algebra belonging to 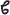. The algebras of 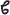, being similar, have the same set of operations. We observe that other operations, called compound operations, may be obtained by composition from the assigned operations.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 3 , Issue 2 , 01 May 1960 , pp. 131 - 132
Copyright
Copyright © Canadian Mathematical Society 1960

References

1. Lambek, J., Goursat's theorem and the Zassenhaus lemma, Canad. J. Math. 10 (1957), 45-56.Google Scholar