Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T14:57:24.552Z Has data issue: false hasContentIssue false
  • English
  • Français

A Relation Between S1 and S3-Invariant Homotopy In The Stable Range

Published online by Cambridge University Press:  20 November 2018

Shirley M. F. Gilbert  and
Peter Zvengrowski
Shirley M. F. Gilbert
Affiliation:
The University of Calgary Calgary, Alberta
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any X and any q > 0, one has natural inclusions 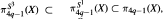where the groups S1 and S3 act on S4q-1 in the standard way and 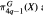are the G-invariant homotopy subsets, G = S1 or G = S3. It is proved here that for any space X of the homotopy type of a CW-complex and for π4q-1 (X) in the c3 cl stable range, the inclusion 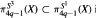is m fact an equality when localized away from the prime 2.

Keywords

55Q4055Q4555Q52.
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 1 , 01 March 1992 , pp. 75 - 80
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Atiyah, M. F., Thom complexes, Proc. London Math. Soc. 11(1961),291–310.Google Scholar
2. Harris, B., On the homotopy groups of the classical groups, Ann. of Math. 74(1961), 407–413.Google Scholar
3. James, I. M., The topology ofStiefel manifolds, London Math. Soc. Lecture Note Series 24, Cambridge University Press, Cambridge, (1976).Google Scholar
4. Gilbert, S., G-invariant homotopy of spheres, Ph. D. Thesis, Univ. of Calgary, (1980).Google Scholar
5. Gilbert, S. and Zvengrowski, P., Sl -invariant homotopy of spheres, Osaka J. Math. 17(1980),603–617.Google Scholar
6. Mukai, J., Non-Sl -symmetricity of some elements of homotopy groups of spheres, Sci. Rep. Osaka 24( 1975), 7–8.Google Scholar
7. Oshima, H., On F-projective homotopy of spheres, Osaka J. Math. 14(1977),179–189.Google Scholar
8. Oshima, H., On F-projective stable stems, Osaka J. Math. 16(1979),505–528.Google Scholar
9. Oshima, H., On C -projective 8 and 10 stems, Osaka J. Math. 17(1980),619–623.Google Scholar
10. Randall, D., F-projective homotopy and F-projective stable stems, Duke Math. J. 42(1975),99–104.Google Scholar
11. Rees, E., Symmetric maps, J. London Math. Soc. 3(1971),267–272.Google Scholar
12. Spanier, E., Infinite symmetric products, function spaces and duality, Ann. of Math. 69(1959),142–198.Google Scholar
13. Steenrod, N. E. and D. Epstein, B. A., Cohomology Operations, Ann. of Math. Studies 50, Princeton University Press, Princeton, (1962).Google Scholar
14. J. Whitehead, H. C., On the groups irr(Vn,m) and sphere bundles, Proc. London Math. Soc. 48(1944),243–291.Google Scholar